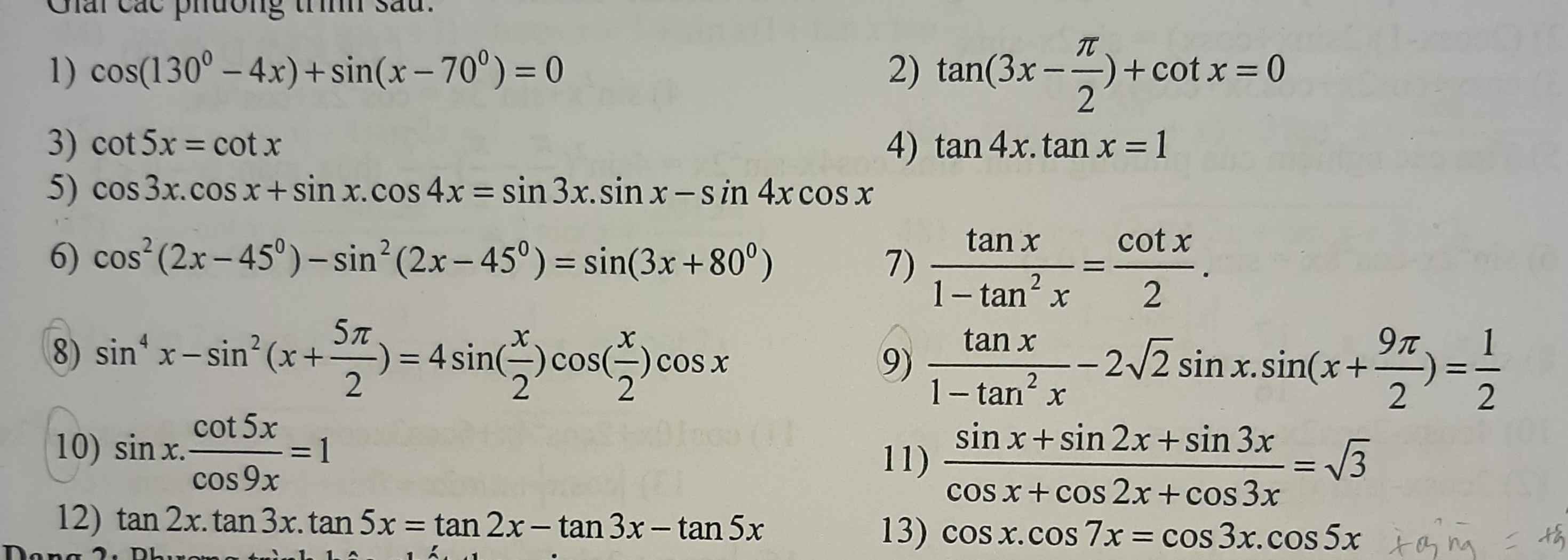8.
\(\Leftrightarrow sin^4x-cos^2x=2sinx.cosx\)
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^4x\) ta được:
\(tan^4x-\dfrac{1}{cos^2x}=2tanx.\dfrac{1}{cos^2x}\)
\(\Leftrightarrow tan^4x-\left(1+tan^2x\right)=2tanx\left(1+tan^2x\right)\)
\(\Leftrightarrow tan^4x-2tan^3x-tan^2x-2tanx-1=0\)
Wel well, đề bài sai, phương trình bậc 4 này không giải được
9.
ĐKXĐ: \(\left[{}\begin{matrix}x\ne\pm\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\dfrac{cos^2x.tanx}{cos^2x\left(1-tan^2x\right)}-2\sqrt{2}sinx.cosx=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{sinx.cosx}{cos^2x-sin^2x}-\sqrt{2}sin2x=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{sin2x}{cos2x}-2\sqrt{2}sin2x=1\)
\(\Leftrightarrow sin2x-2\sqrt{2}sin2x.cos2x=cos2x\)
\(\Leftrightarrow sin2x-cos2x=\sqrt{2}sin4x\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)=\sqrt{2}sin4x\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)=sin4x\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=2x-\dfrac{\pi}{4}+k2\pi\\4x=\dfrac{5\pi}{4}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{8}+k\pi\\x=\dfrac{5\pi}{16}+\dfrac{k\pi}{6}\end{matrix}\right.\)
10.
ĐKXĐ: \(\left[{}\begin{matrix}x\ne\dfrac{k\pi}{5}\\x\ne\dfrac{\pi}{18}+\dfrac{k\pi}{9}\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{sinx.cos5x}{sin5x.cos9x}=1\)
\(\Leftrightarrow sinx.cos5x=sin5x.cos9x\)
\(\Leftrightarrow\dfrac{1}{2}sin6x-\dfrac{1}{2}sin4x=\dfrac{1}{2}sin14x-\dfrac{1}{2}sin4x\)
\(\Leftrightarrow sin14x=sin6x\)
\(\Leftrightarrow\left[{}\begin{matrix}14x=6x+k2\pi\\14x=\pi-6x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{4}\\x=\dfrac{\pi}{20}+\dfrac{k\pi}{10}\end{matrix}\right.\)
12.
ĐKXĐ: ...
\(\Leftrightarrow tan3x+tan5x=tan2x-tan2x.tan3x.tan5x\)
\(\Leftrightarrow tan3x+tan5x=tan2x\left(1-tan3x.tan5x\right)\)
\(\Rightarrow tan2x=\dfrac{tan3x+tan5x}{1-tan3x.tan5x}\)
\(\Rightarrow tan2x=tan8x\)
\(\Rightarrow8x=2x+k\pi\)
\(\Rightarrow x=\dfrac{k\pi}{6}\)
ĐKXĐ:
2. (do \(tan\left(3x-\dfrac{\pi}{2}\right)=-cot3x\))
Nên ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\sin3x\ne0\end{matrix}\right.\) \(\Leftrightarrow sin3x\ne0\) (do trong công thức \(sin3x\) bao hàm nhân tử \(sinx\))
\(\Leftrightarrow3x\ne k\pi\Rightarrow x\ne\dfrac{k\pi}{3}\)
7.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\tan^2x\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\tanx\ne\pm1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\pm\dfrac{\pi}{4}+n\pi\end{matrix}\right.\)