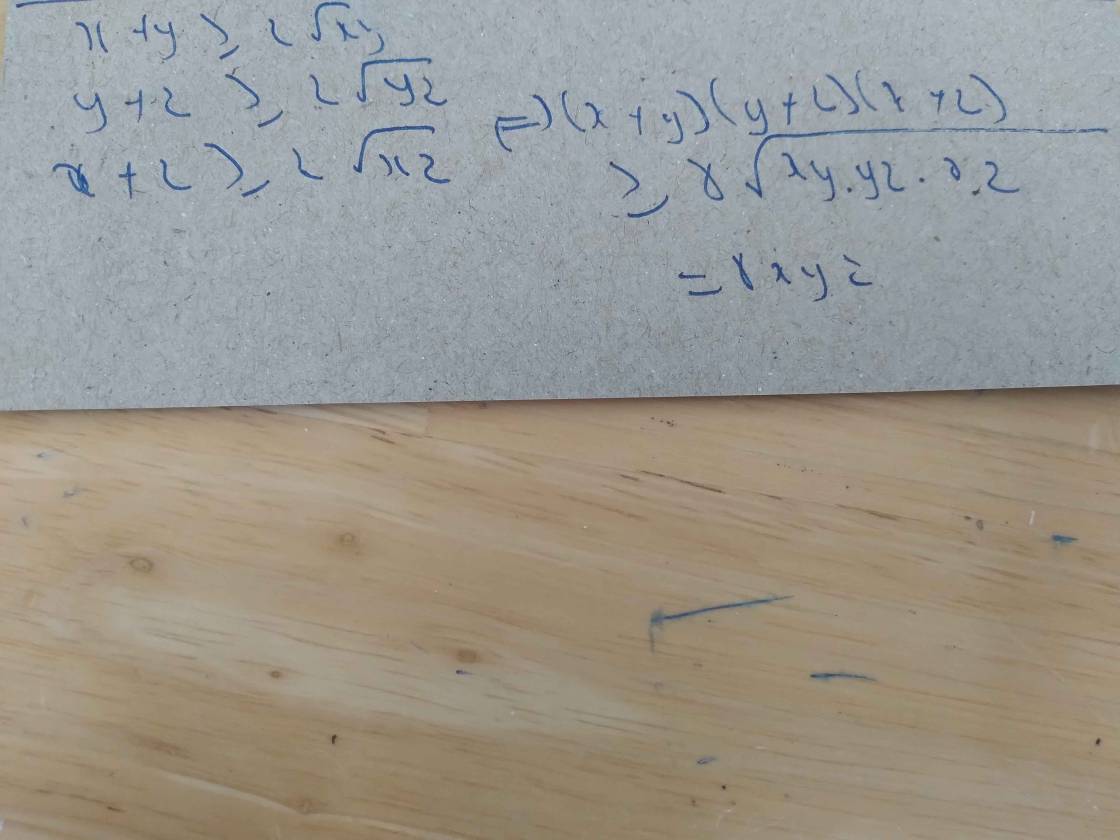21 tháng 4 2023 lúc 22:18
Các câu hỏi tương tự
Cho x,y,z là các số dương thỏa mãn (x+y)(y+z)(z+x)=8xyz
CMR: x=y=z
cho x,y,z dương thoả mãn điều kiện : (x+y)(y+z)(z+x)=8xyz.
CMR x=y=z
cho x> 0 , y>0 , z>0
CMR: (x+y)(y+z)(x+z) > 8xyz
cho x,y,z không âm cmr : x(x-y)^2+y(y-z)^2>=(x-y)(y-z)(x+y-z)
Cho x; y; z là độ dài ba cạnh của tam giác ABC . Biết : (x+y)(y+z)(z+x)=8xyz. CMR: tam giác ABC là tam giác đều .
Cho x,y,z là các số nguyễn dương thỏa mãn: \(\left(x+y\right)\left(y+z\right)\left(z+x\right)=8xyz\)
CMR x=y=z
Với x, y, z là số thực không âm, cmr (x+y-z)(y+z-x)(z+x-y)≤xyz
Cho x, y, z duong thrả (x+y)(y+z(z+x)=8xyz. Chứng minh x=y=z
Cho hỏi cái, sắp phải nộp bài rồi mà vẫn chưa làm được :
1, phân tích đa thức ( 12x^2 - 12xy + 3y^2 ) - 10x( 2x - y ) + 8
2, cho x,y,z > 0 thỏa mãn ( x + y )( y + z ) ( x + z ) = 8xyz. CMR x = y = z