Chương II - Đường tròn
Các câu hỏi tương tự
11 tháng 5 2023 lúc 20:38
cho ΔABD vuông cân tại D và nội tiếp đtròn O. Dựng hình bình hành ABCD; gọi h là chân đường vuông góc kẻ từ D đến AC, K là giao điểm của AC với đtròn O. Cmr:
a/ tứ giác HBCD nội tiếp
b/ DOK=2.BDH
c/ CK.CA=2.BD2
cho tam giác ABC nội tiếp đường tròn tâm O có AD,CF,BE là đường cao giao nhau tại H có M là trung diểm của BC
cm tứ giác BFEC nội tiếptứ giác DFEM nội tiếp
Cho nửa đường tròn tâm O đường kính AB=2R. Vẽ bán kính OC vuông góc với AB. Gọi M là điểm chính giữa cung BC, E là giao điểm AM vs OC. Chứng minh
a, tứ giác MBOE nội tiếp đường tròn
b, ME=MB
c, CM là tiếp tuyến của đường tròn ngoại tiếp tứ giác MBOE
d, tính diện tích tam giác BME theo R
Cho tam giác ABC có 3 góc nhọn nội tiếp (O) các đường cao AD;BE;CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M;N;P Chứng minh
1) Tứ giác CEHD nội tiếp
2) 4 điểm B;C;E;F cùng nằm trên 1 đường tròn
3) AE.AC=AH.AD AD.BC=BE.AC
4) H và M đối xứng nhau qua BC xác định tâm đường tròn nội tiếp tam giác DEF
19 tháng 10 2021 lúc 21:47
Cho tam giác ABC nhọn nội tiếp (O) đường cao AK, trực tâm H.
a, CM: AK.HK = KB.KC.
b, Kẻ AD là đường kính. CM tứ giác ABCD là hình bình hành.
c, Kẻ OM vuông góc BC. CM: AH = 2MO.
22 tháng 1 2019 lúc 10:11
cho tam giác ABC nhọn nội tiếp đường tròn \(\left(O;R\right)\), có BC =\(R\sqrt{3}\) và AB < AC.Gọi H là twujc tâm của tam giác ABC nói AH cắt đường tròn tại điểm D khác A
Tính góc BAC suy ra tam giác OAH cân
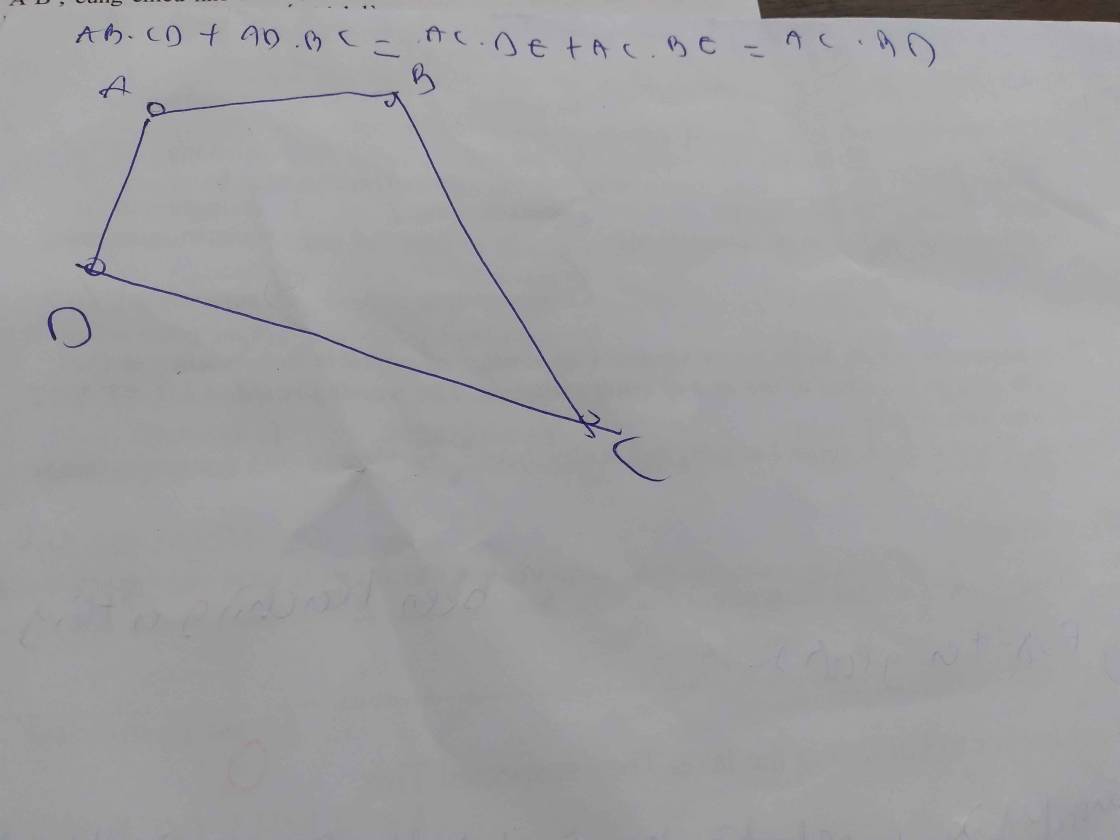
b/ chứng minh rawndg AD.BC=AB.CD + AC.BD
cho tam giác ABC, nội tiếp đường tròn O. hai dường cao BD và CE cắt nhau tại H. tia BD cắt đường tròn tại M. tia CE cắt đường tròn tại N
Chứng minh
a. tứ giác BCDE nội tiếp
b, tam giác ADB đồng rạng với tam giác ACE, từ đó suy ra AE.AB = AB.AC
c, AO vuông góc với MN
cho 2 đường tròn o và o tiếp xúc ngoài tại a. Trên tia Ax vuông góc với OO' lấy một điểm M. Vẽ tiếp tuyến MB với đường tròn (O),tiếp tuyến MC với đường tròn (O'), tia BO cắt tia CO tại N a. Chứng minh : MA=MB=MC b. Chứng minh tứ giác MBNC nội tiếp c. Chứng minh BC ⊥ MN
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O). Gọi D là trung điểm OC. Tia AD cắt đường tròn (O) tại M. Tia AC cắt tia BM tại N. a. Chứng minh tứ giác ABMC nội tiếp đường tròn b. Chứng minh NA.NC = NB.NM