Các câu hỏi tương tự
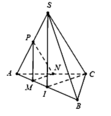
Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng α song song với (SIC). Thiết diện tạo bởi và tứ diện S.ABC là:
A. hình bình hành.
B. tam giác cân tại M.
C. tam giác đều.
D. hình thoi.
Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng
α
song song với
S
C
I
. Tính chu vi của thiết diện tạo bởi
α
và tứ diện S.ABC tính theo
A
M
a
. A.
a
1
+
3
B....
Đọc tiếp
Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng α song song với S C I . Tính chu vi của thiết diện tạo bởi α và tứ diện S.ABC tính theo A M = a .
A. a 1 + 3
B. 2 a 1 + 3
C. 3 a 1 + 3
D.Không tính được
Cho hình chóp
S
.
A
B
C
có M là điểm di động trên cạnh SA sao cho
S
M
S
A
k
. Gọi (α) là mặt phẳng đi qua M và song song với mặt phẳng
A
B
C
. Tìm k để mặt phẳng (α) cắt hình chóp
S
.
A
B
C
theo mộ...
Đọc tiếp
Cho hình chóp S . A B C có M là điểm di động trên cạnh SA sao cho S M S A = k . Gọi (α) là mặt phẳng đi qua M và song song với mặt phẳng A B C . Tìm k để mặt phẳng (α) cắt hình chóp S . A B C theo một thiết diện có diện tích bằng một nửa diện tích tam giác ABC.
A. k = 2 2 .
B. k = 1 2 .
C. k = 3 2 .
D. k = 1 3 .
Cho hình chóp S.ABC có đáy ABC vuông cân tại B với AB a, SA
a
3
và SA
⊥
(ABC). Gọi M là điểm trên cạnh AB và AM x (0 x a), mặt phẳng (
α
) đi qua M và vuông góc với AB. Tìm x để diện tích thiết diện tạo bởi mặt phẳng (
α
) và hình chóp S.ABC lớn nhất A.
x
a
3
B.
x
a
4...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC vuông cân tại B với AB = a, SA = a 3 và SA ⊥ (ABC). Gọi M là điểm trên cạnh AB và AM = x (0 < x < a), mặt phẳng ( α ) đi qua M và vuông góc với AB. Tìm x để diện tích thiết diện tạo bởi mặt phẳng ( α ) và hình chóp S.ABC lớn nhất
A. x = a 3
B. x = a 4
C. x = 2 a 3
D. x = a 2
Cho tứ diện ABCD. Điểm M thuộc đoạn AC M (khác A M, khác C). Mặt phẳng α đi qua M song song với AB và AD. Thiết diện của α với tứ diện ABCD là hình gì?
A. Hình tam giác.
B. Hình bình hành.
C. Hình vuông
D. Hình chữ nhật.
Cho tứ diện ABCD có AB a, CD b. Gọi I, J lần lượt là trung điểm của AB và CD, giả sử
A
B
⊥
C
D
. Mặt phẳng
α
qua M nằm trên đoạn IJ và song song với AB và CD. Tính diện tích thiết diện của tứ diện ABCD với mặt phẳng
α
biết
I
M
1
3
I
J
A. ab B.
a
b...
Đọc tiếp
Cho tứ diện ABCD có AB = a, CD = b. Gọi I, J lần lượt là trung điểm của AB và CD, giả sử A B ⊥ C D . Mặt phẳng α qua M nằm trên đoạn IJ và song song với AB và CD. Tính diện tích thiết diện của tứ diện ABCD với mặt phẳng α biết I M = 1 3 I J
A. ab
B. a b 9
C. 2ab
D. 2 a b 9
Cho tứ diện ABCD. Điểm M thuộc đoạn AC (M khác A, M khác C). Mặt phẳng α đi qua M song song với AB và AD. Thiết diện của α với tứ diên ABCD là hình gì?
A. hình tam giác
B. hình bình hành
C. hình vuông
D. hình chữ nhật
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, CH vuông góc tại H, I là trung điểm của HC. Biết SI vuông góc với mặt phẳng đáy, Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, CH vuông góc tại H, I là trung điểm của HC. Biết SI vuông góc với mặt phẳng đáy, . Gọi O là trung điểm của đoạn AB, O là tâm mặt cầu ngoài tiếp tứ diện SABI. Góc tạo bởi đường thẳng OO và mặt phẳng (ABC) là. Gọi O là trung điểm của đoạn AB, O là tâm mặt cầu ngoài tiếp tứ diện SABI. Góc tạo bởi đường thẳng...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, CH vuông góc tại H, I là trung điểm của HC. Biết SI vuông góc với mặt phẳng đáy, Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, CH vuông góc tại H, I là trung điểm của HC. Biết SI vuông góc với mặt phẳng đáy, . Gọi O là trung điểm của đoạn AB, O' là tâm mặt cầu ngoài tiếp tứ diện SABI. Góc tạo bởi đường thẳng OO' và mặt phẳng (ABC) là. Gọi O là trung điểm của đoạn AB, O' là tâm mặt cầu ngoài tiếp tứ diện SABI. Góc tạo bởi đường thẳng OO' và mặt phẳng (ABC) là
A. 45 ° A S B ^ = 90 °
B. 90 °
C. 30 °
D. 60 °
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác vuông tại A,
S
A
a
3
,
S
B
2
a
Điểm M nằm trên đoạn AD sao cho AM2MD. Gọi (P) là mặt phẳng qua M và song song với (SAB). Tính diện tích thiết diện của hình chóp cắt bởi phẳng (P)? A.
5
a
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác vuông tại A, S A = a 3 , S B = 2 a Điểm M nằm trên đoạn AD sao cho AM=2MD. Gọi (P) là mặt phẳng qua M và song song với (SAB). Tính diện tích thiết diện của hình chóp cắt bởi phẳng (P)?
A. 5 a 2 3 18
B. 5 a 2 3 6
C. 4 a 2 3 9
D. 4 a 2 3 3