Các câu hỏi tương tự
Cho tứ diện ABCD, G là trọng tâm tứ diện. Gọi
G
1
là giao điểm của AG và mp(BCD),
G
2
là giao điểm của BG và mp(ACD). Khẳng định nào sau đây là đúng? A.
G
1
G
2
/
/
A
B
B.
G
1
G
2
/
/...
Đọc tiếp
Cho tứ diện ABCD, G là trọng tâm tứ diện. Gọi G 1 là giao điểm của AG và mp(BCD), G 2 là giao điểm của BG và mp(ACD). Khẳng định nào sau đây là đúng?
A. G 1 G 2 / / A B
B. G 1 G 2 / / A C
C. G 1 G 2 / / C D
D. G 1 G 2 / / A D
Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm các tam giác BCD và ACD. Trong các khẳng định sau, khẳng định nào sai? A.
G
1
G
2
2
3
A
B
B.
G
1
G
2
/
/
A
B
D
C.
G...
Đọc tiếp
Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm các tam giác BCD và ACD. Trong các khẳng định sau, khẳng định nào sai?
A. G 1 G 2 = 2 3 A B
B. G 1 G 2 / / A B D
C. G 1 G 2 / / A B C
D. B G 1 , A G 2 và CD đồng qui
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau? A.
A
B
E
⊥
A
D
C
B.
A
B
D
⊥
A...
Đọc tiếp
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?
A. A B E ⊥ A D C
B. A B D ⊥ A D C
C. A B C ⊥ D F K
D. D F K ⊥ A D C
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD. DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau? A.
A
B
E
⊥
A
D
C
B.
A
B
D
⊥
A...
Đọc tiếp
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD. DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?
A. A B E ⊥ A D C
B. A B D ⊥ A D C
C. A B C ⊥ D F K
D. D F K ⊥ A D C
Cho tứ diện ABCD. Gọi
G
1
và
G
2
lần lượt là trọng tâm các tam giác BCD và ACD. Khẳng định nào sau đây là sai? A.
G
1
G
2
//(ABD) B.
G
1
G
2
//(ABC) C. B
G
1
, A
G
2...
Đọc tiếp
Cho tứ diện ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm các tam giác BCD và ACD. Khẳng định nào sau đây là sai?
A. G 1 G 2 //(ABD)
B. G 1 G 2 //(ABC)
C. B G 1 , A G 2 và CD đồng quy
D. G 1 G 2 = 2 3 A B
Cho tứ diện ABCD có hai mặt ABC và DBC là những tam giác đều cạnh bằng 1,
A
D
2
.
Gọi O là trung điểm cạnh AD. Xét hai khẳng định sau:
(
I
)
O
là tâm mặt cầu ngoại tiếp tứ diện ABCD.
(
I
I
)
O
.
A
B
C
là hình chóp tam giác đều. Hãy chọn khẳng định đúng A. Chỉ (II) đúng B. Cả (I) và (II) đều...
Đọc tiếp
Cho tứ diện ABCD có hai mặt ABC và DBC là những tam giác đều cạnh bằng 1, A D = 2 . Gọi O là trung điểm cạnh AD. Xét hai khẳng định sau:
( I ) O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
( I I ) O . A B C là hình chóp tam giác đều.
Hãy chọn khẳng định đúng
A. Chỉ (II) đúng
B. Cả (I) và (II) đều sai
C. Cả (I) và (II) đều đúng
D. Chỉ (I) đúng
Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC, ABD. Khẳng định nào sau đây đúng ? A. IJ//CD và
I
J
2
3
C
D
B. IJ//AB và
I
J
2
3
A
B
C. IJ//AB và
I
J
1
3
A
B
D. IJ//CD và
I
J
1...
Đọc tiếp
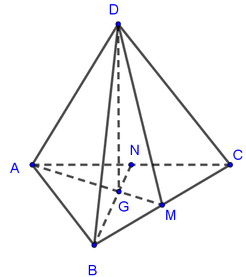
Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC, ABD. Khẳng định nào sau đây đúng ?
A. IJ//CD và I J = 2 3 C D
B. IJ//AB và I J = 2 3 A B
C. IJ//AB và I J = 1 3 A B
D. IJ//CD và I J = 1 3 C D
Trong không gian cho tứ diện ABCD có I, J là trọng tâm các tam giác ABC, ABD. Khẳng định nào sau đây là đúng? A.
I
J
/
/
B
C
D
B.
I
J
/
/
A
B
C
C.
I
J
/
/
A
B
D
D. ...
Đọc tiếp
Trong không gian cho tứ diện ABCD có I, J là trọng tâm các tam giác ABC, ABD. Khẳng định nào sau đây là đúng?
A. I J / / B C D
B. I J / / A B C
C. I J / / A B D
D. I J / / B I J
Cho tứ diện ABCD, gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Khẳng định nào sau đây là sai? A.
I
J
⊥
C
D
D. IC và JD đồng quy tại 1 điểm
Đọc tiếp
Cho tứ diện ABCD, gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Khẳng định nào sau đây là sai?
A. I J ⊥ C D
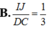
![]()
D. IC và JD đồng quy tại 1 điểm