Đáp án A.
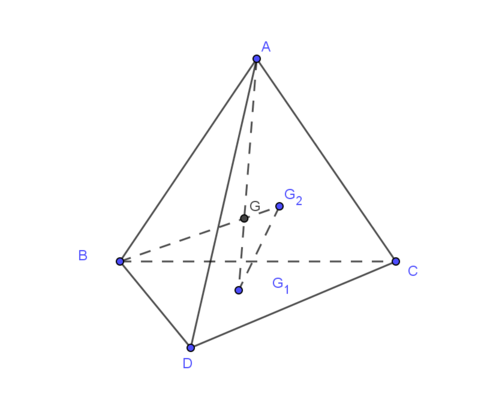
Hình vẽ dễ thấy tính song song là: G 1 G 2 ∥ A B
Chứng minh
Vì G G 1 G A = G G 2 G B = 1 4 ⇒ G 1 G 2 ∥ A B
Đáp án A.

Hình vẽ dễ thấy tính song song là: G 1 G 2 ∥ A B
Chứng minh
Vì G G 1 G A = G G 2 G B = 1 4 ⇒ G 1 G 2 ∥ A B
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AD, BC; G là trọng tâm của tam giác BCD. Khi đó, giao điểm của đường thẳng MG và mp (ABC) là:
A. Giao điểm của đường thẳng MG và đường thẳng AN
B. Điểm N
C. Giao điểm của đường thẳng MG và đường thẳng BC
D. Điểm A
Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD) là
A. điểm F
B. giao điểm của đường thẳng EG và AC
C. giao điểm của đường thẳng EG và CD
D. giao điểm của đường thẳng EG và AF
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm AD và AC. Gọi G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng:
A. Qua M và song song với AB
B. Qua N và song song với BD
C. Qua G và song song với CD
D. Qua G và song song với BC
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm sao cho A S ¯ = B G ¯ . Thể tích của khối đa diện SABCD là
A. a 3 2 12
B. a 3 2 24
C. 5 a 3 2 36
D. 3 a 3 2 24
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD, BC. Gọi G là trọng tâm ∆ B C D Khi đó, giao điểm của đường thẳng MG và mặt phẳng (ABC) là giao điểm của đường thẳng MG và đường thẳng
A. BC
B. AC
C. AN
D. AB
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm đối xứng của G mặt phẳng (ABC). Thể tích khối đa diện SABCD là:
A. a 3 2
B. a 3 2 3
C. a 3 2 6
D. a 3 2 9
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
A. 7 a 2 3 48
B. 7 a 2 3 24
C. a 2 3 16
D. a 2 3 48
Cho tứ diện đều ABCD. Gọi G là trọng tâm tam giác ABC. Chọn khẳng định đúng trong các khẳng định sau:
A. BG ⊥ ACD
B. DG ⊥ ACB
C. DA ⊥ ABC
D. AG ⊥ BCD
Trong không gian Oxyz , cho điểm G - 1 ; 2 ; - 1 . Mặt phẳng (a) đi qua G và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho G là trọng tâm của DABC . Điểm nào sau đây thuộc mặt phẳng (a) ?
A. N - 3 ; 4 ; 2
B. P - 3 ; - 4 ; 2
C. Q 3 ; 4 ; 2
D. M 3 ; 4 ; - 2