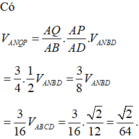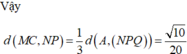Các câu hỏi tương tự
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai đường thẳng MG và NP. Khi đó cosα bằng A.
2
6
B.
2
4
C.
3
6
D.
3
4
Đọc tiếp
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai đường thẳng MG và NP. Khi đó cosα bằng
A. 2 6
B. 2 4
C. 3 6
D. 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB2a, BCa. Các cạnh bên của hình chóp bằng nhau và bằng
a
2
. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD2KA. Tính khoảng cách giữa hai đường thẳng MN và SK. A.
3
a
2
B.
a
2
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
A. 3 a 2
B. a 2 3
C. a 3 7
D. a 21 7
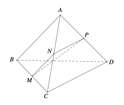
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CA và AD (tham khảo hình vẽ bên). Biết
M
N
P
^
150
0
. Góc giữa hai đường thẳng AB và CD là A. 30
°
B. 45
°
C. 90
°
D. 60
°
Đọc tiếp
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CA và AD (tham khảo hình vẽ bên). Biết M N P ^ = 150 0 . Góc giữa hai đường thẳng AB và CD là
A. 30 °
B. 45 °
C. 90 °
D. 60 °
Cho tứ diện đều ABCD, gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi là số đo của góc giữa hai đường thẳng AN, CM. Khi đó cosα bằng
A. 2 3
B. 1 3
C. 1
D. 2
Cho tứ diện ABCD gọi M, N lần lượt là trung điểm của BC và AD. Biết
A
B
C
D
a
,
M
N
a
3
2
. Tính góc giữa hai đường thẳng AB và CD. A.
45
°
B.
30
°
C.
60
°
D.
90
°
Đọc tiếp
Cho tứ diện ABCD gọi M, N lần lượt là trung điểm của BC và AD.
Biết A B = C D = a , M N = a 3 2 . Tính góc giữa hai đường thẳng AB và CD.
A. 45 °
B. 30 °
C. 60 °
D. 90 °
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho
P
B
P
A
2018
2017
. Tính thể tích V của khối tứ diện PMNC. A.
27.
2
12
B.
9.2018....
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho P B P A = 2018 2017 . Tính thể tích V của khối tứ diện PMNC.
A. 27. 2 12
B. 9.2018. 2 16.2017
C. 9. 2 16
D. 9.2017. 2 16.2018
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD; H là giao điểm của CN với DM. Biết SH vuông góc với mặt phẳng (ABCD) và
S
H
a
3
.
Tính khoảng cách giữa hai đường thẳng DM và SC theo a. A.
2
3
a
19
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD; H là giao điểm của CN với DM. Biết SH vuông góc với mặt phẳng (ABCD) và S H = a 3 . Tính khoảng cách giữa hai đường thẳng DM và SC theo a.
A. 2 3 a 19
B. 2 3 a 19
C. 3 a 19
D. 3 3 a 19
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD 2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD = 2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD.
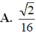
![]()
![]()
![]()
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M,N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD A.
2
/16. B. 23
2
/432. C.
2
/48. D. 13
2
/432.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M,N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD=2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD
A. 2 /16.
B. 23 2 /432.
C. 2 /48.
D. 13 2 /432.