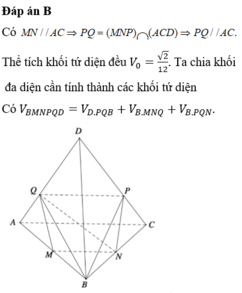
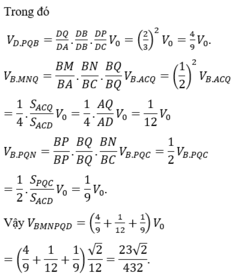Các câu hỏi tương tự
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD 2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD = 2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD.
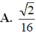
![]()
![]()
![]()
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho PC2PD. Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng A.
11
2
216
B.
2
27
C.
5
2
108
D.
7...
Đọc tiếp
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho PC=2PD. Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng
A. 11 2 216
B. 2 27
C. 5 2 108
D. 7 2 216
Cho tứ diện ABCD có thể tích bằng 3. Gọi N, P lần lượt là trung điểm của BC, CD; M là điểm đoạn AB sao cho
B
M
2
A
M
. Mặt phẳng (MNP) cắt AD tại Q. Thể tích khối đa diện AMQPCN bằng A.
7
3
B.
15
16
C.
7
6
D.
15
8
Đọc tiếp
Cho tứ diện ABCD có thể tích bằng 3. Gọi N, P lần lượt là trung điểm của BC, CD; M là điểm đoạn AB sao cho B M = 2 A M . Mặt phẳng (MNP) cắt AD tại Q. Thể tích khối đa diện AMQPCN bằng
A. 7 3
B. 15 16
C. 7 6
D. 15 8
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V A.
11
2
a
3
216
B.
7...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V. A.
11
2
a
3
216
B.
7
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 18
D. 13 2 a 3 216
Cho tứ diện ABCD,M,N lần lượt là trung điểm của AB và BC, P là điểm trên cạnh CD sao cho CP=2PD Mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số A Q Q D .
A. 1 2
B. 3
C. 2 3
D. 2
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm AB, BC và điểm P là điểm đối xứng với B qua D. Mặt phẳng (MNP) chia tứ diện thành hai phần có tỉ số thể tích là A.
1
2
B.
7
11
C.
7
18
D.
11
18
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm AB, BC và điểm P là điểm đối xứng với B qua D. Mặt phẳng (MNP) chia tứ diện thành hai phần có tỉ số thể tích là
A. 1 2
B. 7 11
C. 7 18
D. 11 18
Cho tứ diện ABCD, M, N lần lượt là trung điểm của AB,BC. P là điểm trên cạnh AC sao cho CP2PD. Mặt phẳng (MNP) cắt AD tại Q. Tính
A
Q
Q
D
A. 1/2 B. 3 C.2/3 D. 2
Đọc tiếp
Cho tứ diện ABCD, M, N lần lượt là trung điểm của AB,BC. P là điểm trên cạnh AC sao cho CP=2PD. Mặt phẳng (MNP) cắt AD tại Q. Tính A Q Q D
A. 1/2
B. 3
C.2/3
D. 2
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho
P
B
P
A
2018
2017
. Tính thể tích V của khối tứ diện PMNC. A.
27.
2
12
B.
9.2018....
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho P B P A = 2018 2017 . Tính thể tích V của khối tứ diện PMNC.
A. 27. 2 12
B. 9.2018. 2 16.2017
C. 9. 2 16
D. 9.2017. 2 16.2018