Các câu hỏi tương tự
Cho tứ diện ABCD, M, N lần lượt là trung điểm của AB,BC. P là điểm trên cạnh AC sao cho CP2PD. Mặt phẳng (MNP) cắt AD tại Q. Tính
A
Q
Q
D
A. 1/2 B. 3 C.2/3 D. 2
Đọc tiếp
Cho tứ diện ABCD, M, N lần lượt là trung điểm của AB,BC. P là điểm trên cạnh AC sao cho CP=2PD. Mặt phẳng (MNP) cắt AD tại Q. Tính A Q Q D
A. 1/2
B. 3
C.2/3
D. 2
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho PC2PD. Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng A.
11
2
216
B.
2
27
C.
5
2
108
D.
7...
Đọc tiếp
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho PC=2PD. Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng
A. 11 2 216
B. 2 27
C. 5 2 108
D. 7 2 216
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD 2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD.
Đọc tiếp
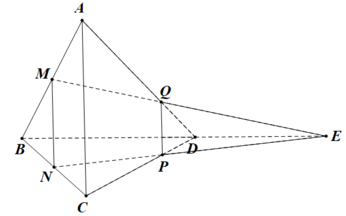
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD = 2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD.
![]()
![]()
![]()
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M,N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD A.
2
/16. B. 23
2
/432. C.
2
/48. D. 13
2
/432.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M,N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD=2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD
A. 2 /16.
B. 23 2 /432.
C. 2 /48.
D. 13 2 /432.
Cho tứ diện ABCD có thể tích bằng 3. Gọi N, P lần lượt là trung điểm của BC, CD; M là điểm đoạn AB sao cho
B
M
2
A
M
. Mặt phẳng (MNP) cắt AD tại Q. Thể tích khối đa diện AMQPCN bằng A.
7
3
B.
15
16
C.
7
6
D.
15
8
Đọc tiếp
Cho tứ diện ABCD có thể tích bằng 3. Gọi N, P lần lượt là trung điểm của BC, CD; M là điểm đoạn AB sao cho B M = 2 A M . Mặt phẳng (MNP) cắt AD tại Q. Thể tích khối đa diện AMQPCN bằng
A. 7 3
B. 15 16
C. 7 6
D. 15 8
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB 2. Xét M là điểm thay đổi trên canh BC. Mặt phẳng (α) qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức
S
M
P
2
+
N
Q
2
bằng A.
8
5
B.
34
9
C.
3
4...
Đọc tiếp
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB = 2. Xét M là điểm thay đổi trên canh BC. Mặt phẳng (α) qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức S = M P 2 + N Q 2 bằng
A. 8 5
B. 34 9
C. 3 4
D. 8 9
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không là trung điểm của BC). Thiết diện của tứ diện bị cắt bởi mặt phẳng M N P là
A. một tứ giác
B. một ngũ giác
C. một lục giác
D. một tam giác
Cho tứ diện ABCD có AB vuông góc với CD, ABCD6. M là điểm thuộc canh BC sao cho MCx.BC (0x1). Mặt phẳng (P) đi qua M và song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Diện tích lớn nhất
S
m
a
x
của tứ giác MNPQ bằng bao nhiêu? A. 9 B. 4,5 C. 36 D. 18
Đọc tiếp
Cho tứ diện ABCD có AB vuông góc với CD, AB=CD=6. M là điểm thuộc canh BC sao cho MC=x.BC (0<x<1). Mặt phẳng (P) đi qua M và song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Diện tích lớn nhất S m a x của tứ giác MNPQ bằng bao nhiêu?
A. 9
B. 4,5
C. 36
D. 18
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm AB, BC và điểm P là điểm đối xứng với B qua D. Mặt phẳng (MNP) chia tứ diện thành hai phần có tỉ số thể tích là A.
1
2
B.
7
11
C.
7
18
D.
11
18
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm AB, BC và điểm P là điểm đối xứng với B qua D. Mặt phẳng (MNP) chia tứ diện thành hai phần có tỉ số thể tích là
A. 1 2
B. 7 11
C. 7 18
D. 11 18