Question

cho tứ diện ABCD có G là trọng tâm tam giác ABC và M thuộc cạnh AD sao cho AD=3MD.

a) chứng minh MG//(BCD)

b) tìm giao điểm của DG và (MBC)

Answer 1

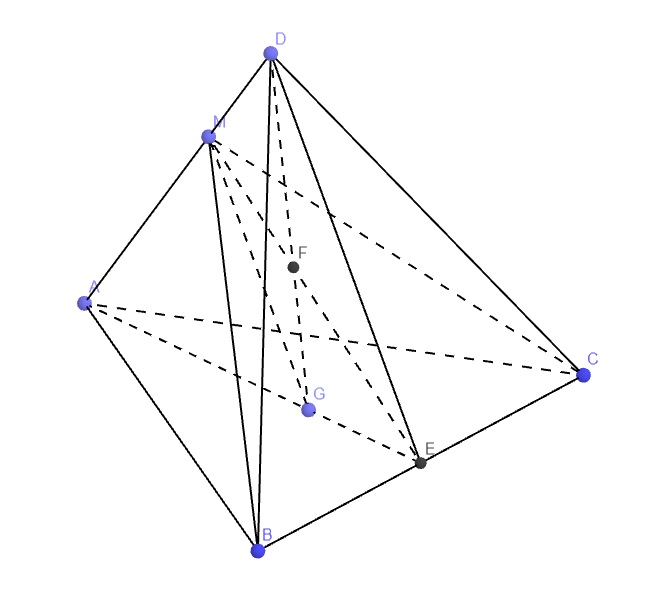
Gọi E là trung điểm BC

Do G là trọng tâm ABC, theo tính chất trọng tâm: \(\dfrac{AG}{AE}=\dfrac{2}{3}\)

\(AD=3MD=3\left(AD-AM\right)\Rightarrow3AD=2AM\Rightarrow\dfrac{AM}{AD}=\dfrac{2}{3}\)

\(\Rightarrow\dfrac{AG}{AE}=\dfrac{AM}{AD}\)

\(\Rightarrow MG||DE\)

Mà DE thuộc (BCD) nên \(MG||\left(BCD\right)\)

b.

\(E\in BC\in\left(MBC\right)\Rightarrow ME\in\left(MBC\right)\)

Trong mp (ADE), nối DG cắt ME tại F

\(\left\{{}\begin{matrix}F\in ME\in\left(MBC\right)\\F\in DG\end{matrix}\right.\)

\(\Rightarrow F=DG\cap\left(MBC\right)\)

Answer 2