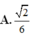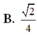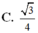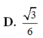Question

Cho tứ diện ABCD có G là trọng tâm của tam giác BCD. Gọi H, K lần lượt là trung điểm của các cạnh AB, AC. Chứng minh rằng

a) vecto BC = 2 vecto Hk

b) vecto AB + vecto AC + vecto AD = 3 vecto AG

Answer 1

a: Xét ΔABC có

H,K lần lượt là trung điểm của AB,AC
=>HK là đường trung bình của ΔABC

=>HK//BC và \(HK=\frac12BC\)

=>\(\overrightarrow{HK}=\frac12\cdot\overrightarrow{BC}\)

=>\(\overrightarrow{BC}=2\cdot\overrightarrow{HK}\)

b: \(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\)
\(=\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{AG}+\overrightarrow{GD}+\overrightarrow{AG}+\overrightarrow{GC}\)

\(=3\cdot\overrightarrow{AG}+\left(\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}\right)=3\cdot\overrightarrow{AG}\)