Các câu hỏi tương tự
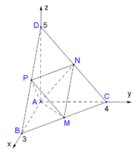
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau
A
B
3
,
A
C
4
,
A
D
5
. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Tính thể tích tứ diện AMNP. A.
15
6
B.
20
7
C.
8
3
D....
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau A B = 3 , A C = 4 , A D = 5 . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Tính thể tích tứ diện AMNP.
A. 15 6
B. 20 7
C. 8 3
D. 5 2
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau;
A
B
6
a
;
A
C
7
a
và
A
D
4
a
. Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích V của tứ diện AMNP A.
V
7
2
a
3
B.
V
7...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; A B = 6 a ; A C = 7 a và A D = 4 a . Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích V của tứ diện AMNP
A. V = 7 2 a 3
B. V = 7 a 3
C. V = 28 3 a 3
D. V = 14 a 3
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau,
A
B
6
a
,
A
C
5
a
,
A
D
4
a
.
Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là: A.
V
5...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, A B = 6 a , A C = 5 a , A D = 4 a . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
A. V = 5 a 3 3 .
B. V = 20 a 3 3 .
C. V = 5 a 3
D. V = 10 a 3
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau,
A
B
6
a
,
A
C
7
a
,
A
D
8
a
.
. Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là: A.
14
a
2
B.
28
a
2
C.
42...
Đọc tiếp
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, A B = 6 a , A C = 7 a , A D = 8 a . . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
A. 14 a 2
B. 28 a 2
C. 42 a 2
D. 7 a 2
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB3a,AC6a,AD4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP A. 3
a
3
B. 12
a
3
C.
a
3
D. 2
a
3
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB=3a,AC=6a,AD=4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng
A
B
a
,
A
C
a
2
,
A
D
a
3
,
a
0
.
Thể tích V của khối tứ diện ABCD là: A.
V
1
3
a
3...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng A B = a , A C = a 2 , A D = a 3 , a > 0 . Thể tích V của khối tứ diện ABCD là:
A. V = 1 3 a 3 6
B. V = 1 6 a 3 6
C. V = 1 2 a 3 6
D. V = 1 9 a 3 6
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB 3a, AC 4a, AD 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a. A.
V
10
a
3
27
B.
V
80
a
3
27
C....
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB = 3a, AC = 4a, AD = 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
A. V = 10 a 3 27
B. V = 80 a 3 27
C. V = 20 a 3 27
D. V = 40 a 3 27
Cho tứ diện ABCD có các cạnh BA,BC,BD đôi một vuông góc với nhau,
B
A
3
a
B
C
B
D
2
a
.
Gọi M,N lần lượt là trung điểm của
A
B
v
à
A
D
. Tính thể tích khối chóp A.
V
8
a
3
B.
V...
Đọc tiếp
Cho tứ diện ABCD có các cạnh BA,BC,BD đôi một vuông góc với nhau, B A = 3 a B C = B D = 2 a . Gọi M,N lần lượt là trung điểm của A B v à A D . Tính thể tích khối chóp
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 3 a 3 2
D. V = a 3
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau. Gọi
G
1
;
G
2
;
G
3
G
4
lần lượt là trọng tâm các tam giác ABC;ABD;ACD; và BCD. Biết
A
B
6
a
;
A
C
9
a
;
A
D
12
a
. Tính theo a thể tích khối tứ diện
G
1...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau. Gọi G 1 ; G 2 ; G 3 G 4 lần lượt là trọng tâm các tam giác ABC;ABD;ACD; và BCD. Biết A B = 6 a ; A C = 9 a ; A D = 12 a . Tính theo a thể tích khối tứ diện G 1 G 2 G 3 G 4 .
A. 4 a 3
B. a 3
C. 108 a 3
D. 36 a 3