Đáp án D
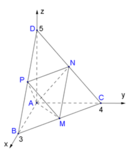
Ta có AB, AC, AD đôi một vuông góc với nhau, do đó chọn hệ trục tọa độ Oxyz như hình vẽ.

Đáp án D

Ta có AB, AC, AD đôi một vuông góc với nhau, do đó chọn hệ trục tọa độ Oxyz như hình vẽ.

Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau AB=3, AC=4, AD=5. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Tính thể tích tứ diện AMNP
A. 5 2
B. 8 3
C. 20 7
D. 15 6
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; A B = 6 a ; A C = 7 a và A D = 4 a . Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích V của tứ diện AMNP
A. V = 7 2 a 3
B. V = 7 a 3
C. V = 28 3 a 3
D. V = 14 a 3
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, A B = 6 a , A C = 5 a , A D = 4 a . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
A. V = 5 a 3 3 .
B. V = 20 a 3 3 .
C. V = 5 a 3
D. V = 10 a 3
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, A B = 6 a , A C = 7 a , A D = 8 a . . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
A. 14 a 2
B. 28 a 2
C. 42 a 2
D. 7 a 2
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB=3a,AC=6a,AD=4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Cho tứ diện ABCD có các cạnh BA,BC,BD đôi một vuông góc với nhau, B A = 3 a B C = B D = 2 a . Gọi M,N lần lượt là trung điểm của A B v à A D . Tính thể tích khối chóp
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 3 a 3 2
D. V = a 3
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng A B = a , A C = a 2 , A D = a 3 , a > 0 . Thể tích V của khối tứ diện ABCD là:
A. V = 1 3 a 3 6
B. V = 1 6 a 3 6
C. V = 1 2 a 3 6
D. V = 1 9 a 3 6
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB = 3a, AC = 4a, AD = 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
A. V = 10 a 3 27
B. V = 80 a 3 27
C. V = 20 a 3 27
D. V = 40 a 3 27
Cho tứ diện ABCD có A B , A C , A D đôi một vuông góc với nhau, A B = a , A C = b , A D = c . Tính thể tích V của khối tứ diện ABCD theo a, b, c
A. V = a b c 2
B. V = a b c 6
C. V = a b c 3
D. V = a b c