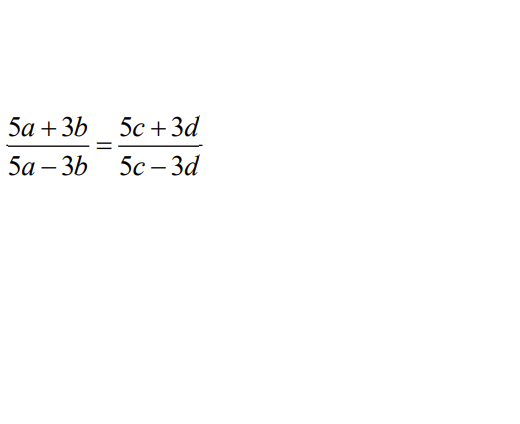Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=kb,=kd\)
\(\Rightarrow\dfrac{5a+3b}{5a-3b}=\dfrac{b\left(5k+3\right)}{b\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\) và \(\dfrac{5c+3d}{5c-3d}=\dfrac{d\left(5k+3\right)}{d\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\)
Vậy \(\dfrac{5a+3b}{5a-3b}=\dfrac{5c+3d}{5c-3d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{5a+3b}{5c+3d}\\\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{5a-3b}{5c-3d}\end{matrix}\right.\)
\(\Rightarrow\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\Rightarrowđpcm\)