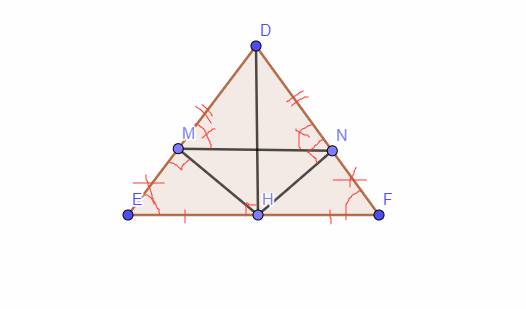
a: Xét ΔDHE và ΔDHF có
DH chung
HE=HF
DE=DF
Do đó: ΔDHE=ΔDHF
b: Sửa đề HK\(\perp\)DF tại K
ΔDHE=ΔDHF
=>\(\widehat{HDE}=\widehat{HDF}\)
Xét ΔDMH vuông tại M và ΔDKH vuông tại K có
DH chung
\(\widehat{MDH}=\widehat{KDH}\)
Do đó: ΔDMH=ΔDKH
=>HM=HK
=>ΔHMK cân tại H
c: ΔDMH=ΔDKH
=>DM=DK
=>D nằm trên đường trung trực của MK(1)
Ta có: HM=HK
=>H nằm trên đường trung trực của MK(2)
Từ (1),(2) suy ra DH là đường trung trực của MK
=>DH\(\perp\)MK
a, Xét Tam giác 𝐻𝐸𝐷HED và Tam giác 𝐻𝐹𝐷HFD có
𝐷𝐸=𝐷𝐹(Tam giaˊc DEF caˆn tại D)DE=DF(Tam giaˊc DEF caˆn tại D)
𝐸^=𝐹^E=F (Tam giaˊc DEF caˆn tại D)(Tam giaˊc DEF caˆn tại D)
=>Tam giaˊc HED = Tam giaˊc HDF (ch-gn)=>Tam giaˊc HED = Tam giaˊc HDF (ch-gn)
𝑏,b, Vì Tam giác 𝐻𝐸𝐷=HED= Tam giác 𝐻𝐹𝐷(𝑎)HFD(a)
−>𝐻𝐸=𝐻𝐹(2 cạnh tương ứng)−>HE=HF(2 cạnh tương ứng)
Xét Tam giác 𝐻𝐸𝑀HEM và Tam giác 𝐻𝐹𝑁HFN có:
𝐻𝐸=𝐻𝐹(𝐶𝑀𝑇)HE=HF(CMT)
𝐸^=𝐹^E=F (𝑎)(a)
𝐸𝑀𝐻^=𝐹𝑁𝐻^=900EMH=FNH=900
=>Tam giaˊc HEM = Tam giaˊc HFN (ch-gn)=>Tam giaˊc HEM = Tam giaˊc HFN (ch-gn)
−>𝐸𝑀=𝐹𝑁(2 cạnh tương ứng)−>EM=FN(2 cạnh tương ứng)
Ta có: {𝐷𝐸=𝑀𝐷+𝑀𝐸𝐷𝐹=𝑁𝐷+𝑁𝐹{DE=MD+MEDF=ND+NF
Mà 𝐷𝐸=𝐷𝐹,𝑀𝐸=𝑁𝐹DE=DF,ME=NF
−>𝑀𝐷=𝑁𝐷−>MD=ND
Xét Tam giác 𝐷𝑀𝑁:𝐷𝑀=𝐷𝑁(𝐶𝑀𝑇)DMN:DM=DN(CMT)
−>Tam giaˊc DMN caˆn tại D−>Tam giaˊc DMN caˆn tại D
−>−>𝐷𝑀𝑁^=𝐷𝑁𝑀^=DMN=DNM=180−𝐴^22180−A
Tam giác 𝐷𝐸𝐹DEF cân tại 𝐷D
−>−>𝐸^=𝐹^=E=F=180−𝐴^22180−A
−>−>𝐷𝑀𝑁^=𝐸^DMN=E
Mà 22 góc này nằm ở vị trí đồng vị
−>MN // EF (t/c 2 đt’ //)−>MN // EF (t/c 2 đt’ //)