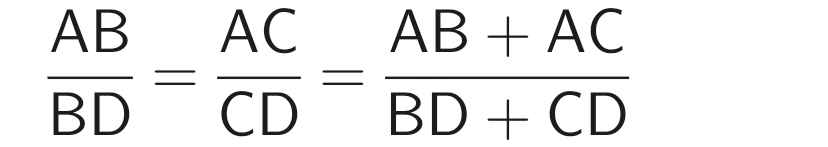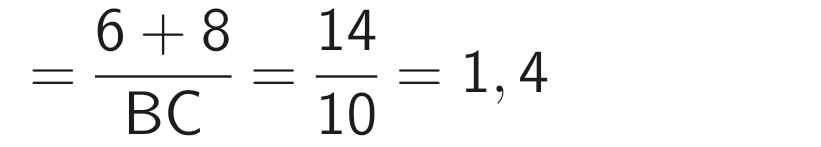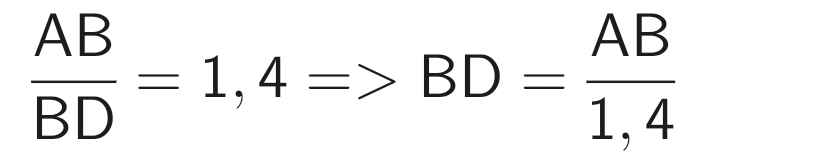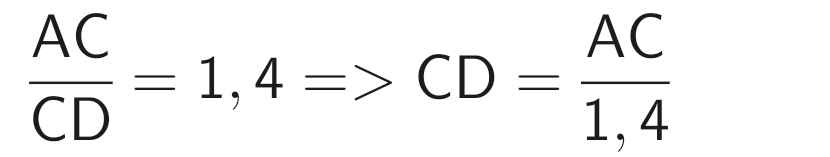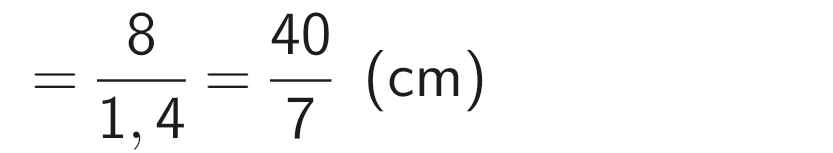Question

Cho tam giác ABC vuông tại A,Đường phân giác AD,biết AB=6cm,BC=10cm.Tính BD,CD

Answer 1

Áp dụng định lý pytago trong \(\Delta ABC\perp\) tại \(A\) có:
          \(AB^2+AC^2=BC^2\)
     \(\Leftrightarrow AC^2=BC^2-AB^2\)
     \(\Leftrightarrow AC^2=10^2-6^2=64\)
     \(\Leftrightarrow AC=8\left(cm\right)\)
Áp dụng tính chất đường phân giác trong \(\Delta ABC\)có:
          \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
    \(\Leftrightarrow\dfrac{DB}{6}=\dfrac{10-DB}{8}\)            \(\left(dk:DB< 10\right)\)
    \(\Rightarrow8DB=60+6DB\)
    \(\Leftrightarrow14DB=60\)
    \(\Leftrightarrow DB=\dfrac{60}{14}=\dfrac{30}{7}\left(cm\right)\) (thỏa mãn)
 Ta co': \(DB+DC=BC\Rightarrow DC=BC-DB\Rightarrow DC=10-\dfrac{30}{7}=\dfrac{40}{7}\left(cm\right)\)
Vậy \(BD=\dfrac{30}{7}cm;CD=\dfrac{40}{7}cm\)
   
 

Answer 2

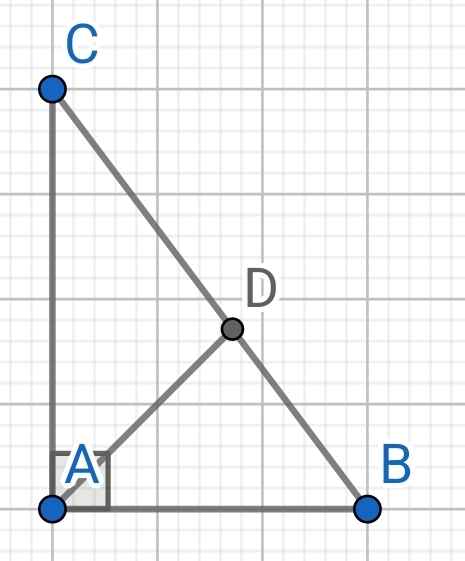
ΔABC vuông tại A (gt)

BC² = AB² + AC² (Pythagore)

AC² = BC² - AB²

= 10² - 6²

= 64

AC = 8 (cm)

ΔABC có AD là đường phân giác (gt)

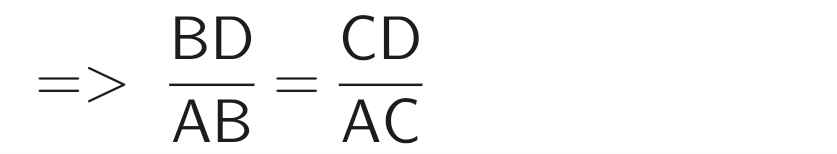
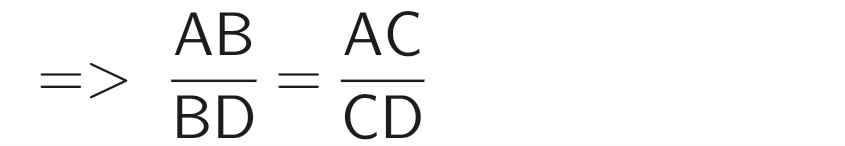
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: