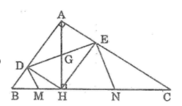
cho tam giác ABC vuông tại A,đường cao AH chia cạnh huyền BC thành 2 đoạn BH và CH có độ dài là 4cm,9cm.D và E là hình chiếu của H trên AB và AC
a)tính DE
b) đường thẳng vuông góc với DE tại D và E.lần lượt cắt BC tại M và N .C/m M là trung điểm của BH và N là trung điểm của CH
c)tính diện tính tứ giác DENM
(giúp mình câu b,c với .mình cảm ơn)
\(b,\) Gọi O là giao điểm ED và AH
\(\Rightarrow OA=OD=OE=OH\\ \Rightarrow\widehat{OEH}=\widehat{OHE}\\ \Rightarrow\widehat{NEH}=\widehat{NHE}\left(\widehat{OEH}+\widehat{NEH}=\widehat{NHE}+\widehat{OHE}=90\right)\\ \Rightarrow NE=EH\left(\Delta NEH.cân\right)\left(1\right)\)
Ta có \(\widehat{NEH}+\widehat{NEC}=90;\widehat{NHE}+\widehat{ECH}=90\Rightarrow\widehat{NEC}=\widehat{EHC}\)
\(\Rightarrow NE=NC\left(\Delta NEC.cân\right)\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow NC=NH\)
\(Cmtt\Leftrightarrow\Delta HMD;\Delta MDB.cân\Leftrightarrow MH=MB\left(=MD\right)\)
\(c,\) Xét tam giác HBD và CEH vuông tại E,D có \(DM=\dfrac{1}{2}HB=2\left(cm\right);EN=\dfrac{1}{2}CH=3\left(cm\right)\)
Áp dụng HTL vào tam giác ABC vuông tại A
\(AH^2=BH\cdot HC=4\cdot9=36\\ \Leftrightarrow AH=6\left(cm\right)\\ \Leftrightarrow DE=AH=6\left(cm\right)\left(hcn.AEHD\right)\)
\(S_{DENM}=\dfrac{1}{2}DE\cdot\left(MD+EN\right)=\dfrac{1}{2}\cdot6\cdot5=15\left(cm^2\right)\)