Xét \(\Delta ABM\) và \(\Delta NBM\)
\(\widehat{MAB}=\widehat{MNB}=90^o\)
\(MB\) chung
\(\widehat{MBA}=\widehat{MBN}\) (vì \(BM\) là tia phân giác của \(\widehat{ABN}\))
suy ra: \(\Delta ABM=\Delta NBM\) (Cạnh huyền-góc nhọn)
\(\Rightarrow\widehat{AMB}=\widehat{NMB}\) (Hai góc tương ứng)
\(\Rightarrow MB\) là tia phân giác của \(\widehat{AMN}\)
Vì \(NK\)//\(BM\) nên \(\widehat{BMN}=\widehat{MNK}\) (hai góc so le trong)
Và \(\widehat{BMA}=\widehat{NKM}\) (đồng vị)
Mà \(\widehat{AMB}=\widehat{NMB}\) (cmt)
Suy ra: \(\widehat{MNK}=\widehat{NKM}\) \(\Rightarrow\Delta MNK\) cân tại \(M\) (đpcm)
a: Xét ΔBAM vuông tại A và ΔBNM vuông tại N có
BM chung
góc ABM=góc NBM
=>ΔBAM=ΔBNM
=>góc AMB=góc NMB
=>MB là phân giác của góc AMN
b: NK//BM
=>góc BMN=góc KNM
=>góc KNM=góc AMB
=>góc MNK=góc MKN
=>ΔKMN cân tại M
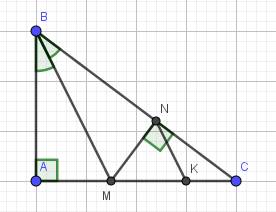
a) Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta NBM\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{NBM}\) (BM là tia phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta ABM=\Delta NBM\) (cạnh huyền - góc nhọn)
\(\Rightarrow\widehat{AMB}=\widehat{NMB}\) (hai góc tương ứng)
\(\Rightarrow MB\) là tia phân giác của \(\widehat{AMN}\)
b) Do NK // BM
\(\Rightarrow\widehat{BMN}=\widehat{MNK}\) (so le trong)
\(\widehat{NKM}=\widehat{AMB}\) (đồng vị)
Mà \(\widehat{AMB}=\widehat{BMN}\) (cmt)
\(\Rightarrow\widehat{MNK}=\widehat{NKM}\)
\(\Delta MNK\) có \(\widehat{MNK}=\widehat{NKM}\) (cmt)
\(\Rightarrow\Delta MNK\) cân tại M














