Question

Cho tam giác ABC vuông tại A, đường cao AH. Gọi M và N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Cm

a) AH^2=AM.AB.

b) AM.AB = AN.AC.

c) Tam giác AMN đồng dạng với tam giác ACB.

(Mình đang cần gấp mong các bạn giúp mình.)

Answer 1

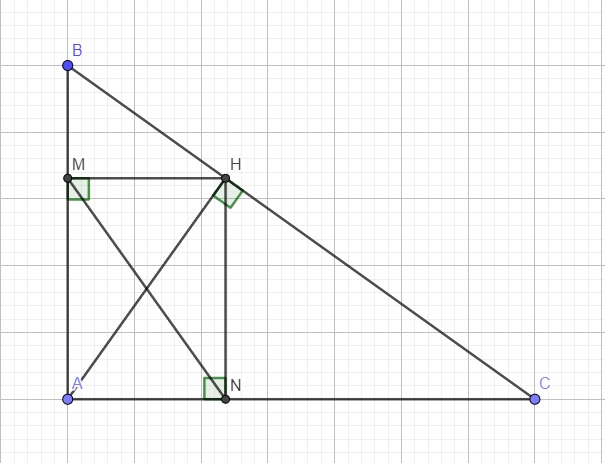
a.

Do \(AH\perp BC\) và \(HM\perp AB\Rightarrow\widehat{AHB}=\widehat{AMH}=90^0\)

Xét hai tam giác AHB và AMH có:

\(\left\{{}\begin{matrix}\widehat{AHB}=\widehat{AMH}=90^0\\\widehat{MAH}-chung\end{matrix}\right.\)

\(\Rightarrow\Delta AHB\sim\Delta AMH\left(g.g\right)\)

\(\Rightarrow\dfrac{AH}{AM}=\dfrac{AB}{AH}\Rightarrow AH^2=AM.AB\) (1)

b. Do \(HN\perp AC\Rightarrow\widehat{ANH}=90^0\)

Xét hai tam giác ANH và AHC có:

\(\left\{{}\begin{matrix}\widehat{ANH}=\widehat{AHC}=90^0\\\widehat{NAH}-chung\end{matrix}\right.\)

\(\Rightarrow\Delta ANH\sim\Delta AHC\left(g.g\right)\)

\(\Rightarrow\dfrac{AN}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AN.AC\) (2)

(1);(2) \(\Rightarrow AM.AB=AN.AC\)

c.

Từ câu b ta suy ra \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)

Xét hai tam giác AMN và ACB có:

\(\left\{{}\begin{matrix}\dfrac{AM}{AC}=\dfrac{AN}{AC}\\\widehat{MAN}-chung\end{matrix}\right.\)

\(\Rightarrow\Delta AMN\sim\Delta ABC\left(c.g.c\right)\)

Answer 2