Question

Cho tam giác ABC vuông tại A, đường cao AH. Gọi 

b. Tam giác DHE là tam giác gì ? Vì sao ?

c. Tứ giác BDEC là hình gì ? Vì sao ?

d. Chứng minh rằng BC = BD + CE.

 

Answer 1

Tk:

 

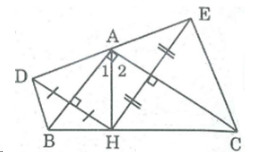
a) Điểm D đối xứng điểm H qua trục AB

⇒ AB là đường trung trực của HD 

⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A

Suy ra: AB là tia phân giác của ˆDAH⇒ˆDAB=ˆA1DAH^⇒DAB^=A^1

Điểm H và điểm E đối xứng qua trục AC

⇒ AC là đường trung trực của HE

⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A

Suy ra: AC là đường phân giác của ˆHAE⇒ˆA2=ˆEACHAE^⇒A^2=EAC^

Ta có: ˆDAE=ˆDAH+ˆHAEDAE^=DAH^+HAE^=2(ˆA1+ˆA2)=2.900=1800=2(A^1+A^2)=2.900=1800

Suy ra D, A, E thẳng hàng

Lại có: AD = AE (vì cùng bằng AH)

Nên điểm A là trung điểm của đoạn DE

Vậy điểm D đối xứng với điểm E qua điểm A.

b) Tam giác DHE có HA là trung tuyến và