Cho tam giác ABC vuông tại A, có đường cao AH, đường trung tuyến AM. Gọi O là trung điểm của AM. Trên tia đối của tia OH lấy điểm K sao cho OK = OH a) Chứng minh tứ giác AHMK là hình chữ nhật b) Trên tia đối của tia MH lấy điểm F sao cho MF = MH Chứng minh tứ giác AMFK là hình bình hành c) Kẻ HQ vuông góc với KF tại Q. Chứng minh: MQ vuông góc với AQ.
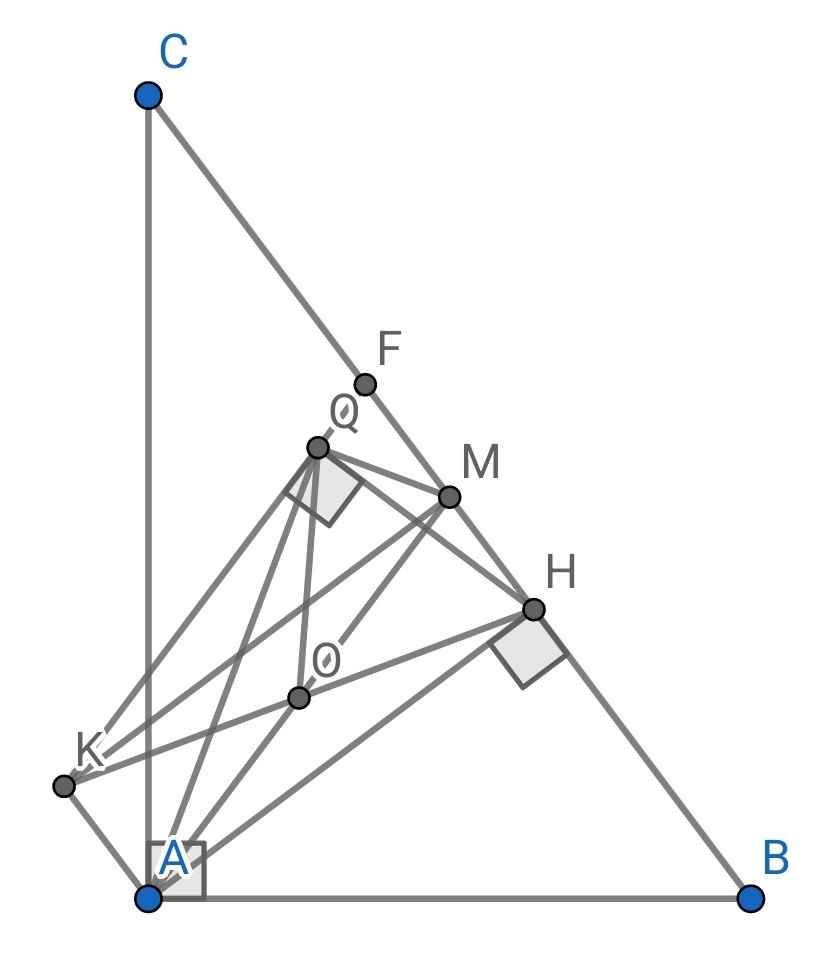 a) Do OH = OK (gt)
a) Do OH = OK (gt)
⇒ O là trung điểm của KH
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ AH ⊥ HM
⇒ ∠AHM = 90⁰
Tứ giác AHMK có:
O là trung điểm của AM (gt)
O là trung điểm của KH (cmt)
⇒ AHMK là hình bình hành
Mà ∠AHM = 90⁰ (cmt)
⇒ AHMK là hình chữ nhật
b) Do AHMK là hình chữ nhật (cmt)
⇒ AK = MH và AK // MH
Do MF = MH (gt)
⇒ AK = MF
Do AK // MH (cmt)
⇒ AK // MF
Tứ giác AMFK có:
AK // MF (cmt)
AK = MF (cmt)
⇒ AMFK là hình bình hành
c) Do AHMK là hình chữ nhật (cmt)
⇒ OA = OH = OM = OK = AM : 2
∆HQK vuông tại Q có OQ là đường trung tuyến
⇒ OQ = OH = HK : 2
Mà OH = OM = OA (cmt)
⇒ OQ = OM = OA = AM : 2
∆AQM có:
OQ là đường trung tuyến (do O là trung điểm của AM)
Mà OQ = OA = OM = AM : 2 (cmt)
⇒ ∆AQM vuông tại Q
⇒ MQ ⊥ AQ







