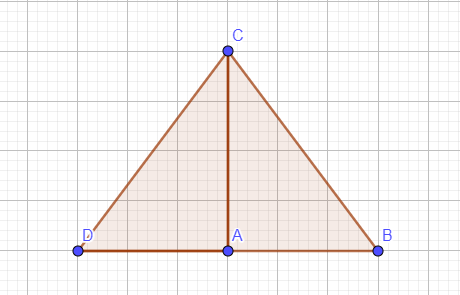
`a)` Áp dụng định lý pytago ta có :
`AB^2+AC^2=BC^2`
hay `9^2+12^2=BC^2`
`=>BC^2=225`
`=>BC=15(cm)`
`b)` Xét `ΔABC` và `ΔADC` ta có :
`AC` chung
`\hat{BAC}=90^o`
`\hat{DAC}=90^o`
`=>ΔABC=ΔADC` (c.g.c)

`a)` Áp dụng định lý pytago ta có :
`AB^2+AC^2=BC^2`
hay `9^2+12^2=BC^2`
`=>BC^2=225`
`=>BC=15(cm)`
`b)` Xét `ΔABC` và `ΔADC` ta có :
`AC` chung
`\hat{BAC}=90^o`
`\hat{DAC}=90^o`
`=>ΔABC=ΔADC` (c.g.c)
Cho ∆ABC vuông tại A có AB < AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB.
a) Chứng minh ABC = ADC.
b) Gọi M là trung điểm của CD. Qua D vẽ đường thẳng song song với BC cắt BM tại E. Chứng minh: ∆CDE cân
c) Gọi I là giao điểm của AC và BE. Chứng minh: BC + BD > IM
Cho tam giác ABC vuông tại A (AB<AC) trên tia đối của tia AB lấy điểm D sao cho AD =AB. chứng minh tam giác ABC = tam giác ADC. Gọi M là trung điểm BC đường thẳng qua B và song song với CD cắt DM tại K chứng minh BK = CD. Qua A kẻ đường thẳng song song với BC cắt CD tại M chứng minh tam giác AMC cân
Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AD = AB
a) Chứng minh Từ đó suy ra cân tại C.
b) Gọi M là trung điểm của CD. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt tia BM tại K. Chứng minh BC = DK và BC + BD > BK
Cho tam giác ABC vuông tại A (AB<AC) có AB=6cm, BC=10cm
a) Tính độ dài AC
b) Trên tia đối của tia AB lấy điểm D sao cho AD=AB. Chứng minh tam giác ABC= tam giác ADC
c) Qua A vẽ đường thẳng song song với BC cắt DC tại E. Chứng minh: tam giác AEC cân tại E
d) Gọi F là trung điểm của BC. Trên AC lấy điểm O sao cho AC=3AO. Chứng minh ba điểm F,O,D thẳng hàng
Giúp mình giải bài này với... Arigatou ^_^
Cho tam giác abc vuông tại a có ab bằng 6cm bc bằng 10cm a tính ac b trên tia đối của tia ab lấy điểm d sao cho ad bằng ab chứng minh Tam giác abc bằng tam giác adc c đường thẳng qua a song song với bc cắt CD tại E chứng minh Tam giác EAC cân
Cho tam giác ABC vuông tại A có AB = 5cm, AC = 12cm.
a. Tính BC
b. Trên tia đối của AB lấy đam giaiểm D sao cho AD = AB. Chứng minh tam giác ABC = tam giác ADC
c. Đường thẳng qua A song song với BC cắt CD tại E. Chứng minnh tam giác EAC cân
d. Gọi F là trung điểm của BC. Chứng minh CA, DF, CE đồng quy tại 1 điểm
Cho tam giác ABC vuông tại A , có AB = 9cm , BC = 15cm . Trên tia đối của AB lấy điểm D sao cho A là trung điểm của BD
a) Tính độ dài AC
b) Chứng minh tam giác ABC bằng tam giác ADC
c) Gọi E là trung điểm của đoạn DC , BE cắt AC tại M . Chứng minh góc MDC bằng góc MBC
d) Từ A vẽ đường thẳng song song với DC , đường này cắt BC tại K . Chứng minh D , M , K thẳng hàng
( Nhớ vẽ hình )
cho dabc vuông tại a có ab < ac . trên tia đối của tia ab lấy điểm d sao cho ad = ab a, so sánh góc B và C b , chứng minh rằng tam giác CBD là tam giác cân c , gọi M là trung điểm của CD , đường thẳng qua D và song song với BC cắt đường thẳng BM tại E . Chứng minh rằng BC = DE và BC + BD > BE
Cho tam giác ABC vuông tại A. Trên tia đối tia AB lấy điểm D sao cho AD = AB.
a/ Cho biết AB = 6cm và BC = 10cm. Tính AC và so sánh góc B và góc C.
b/ Chứng minh tam giác CBD cân.
c/ Gọi M là trung điểm CD. Qua D vẽ đường thẳng song song BC cắt tia BM tại K. Chứng minh BC = DK và BC + BD > BK.
d/ AK cắt DM tại E. Chứng minh BC = 3DE