`@` `\text {dnv4510}`
`a,`
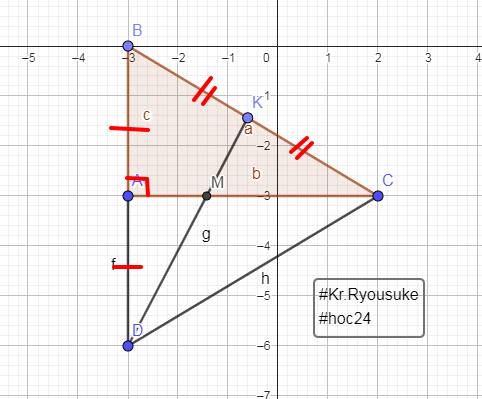
Xét `\Delta ABC:`
`\text {BC > AC > AB (5 cm > 4 cm > 3 cm)}`
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`=>` $\widehat {A} > \widehat {B} > \widehat {C}$.
`b,`
Ta có: A là trung điểm của BD
`-> \text {AC là đường trung tuyến}` `(1)`
K là trung điểm của BC
`-> \text {DK là đường trung tuyến}` `(2)`
Mà \(\text{AC }\cap\text{ DK = M}\) `(3)`
Từ `(1), (2)` và `(3)`
`-> \text {M là trọng tâm của} \Delta ABC`
`@` Theo tính chất của trọng tâm trong `\Delta`
\(\text{MC = }\dfrac{2}{3}\text{AC}\)
Mà \(\text{AC = 4 cm}\)
`->`\(\text{MC = }\dfrac{2}{3}\cdot4=\dfrac{8}{3}\left(\text{cm}\right)\)
Vậy, độ dài của MC là `8/3 cm`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{A là trung điểm của BC}\\\text{AC }\bot\text{ BD}\end{matrix}\right.\)
`->`\(\text{CA là đường trung trực}\)
Ta có: \(\left\{{}\begin{matrix}\text{AC là đường trung trực (hạ từ đỉnh A)}\\\text{AC là đường trung tuyến (hạ từ đỉnh A) }\end{matrix}\right.\)
`@` Theo tính chất của các đường trong `\Delta` với `\Delta` cân
`->` \(\Delta\text{ BDC cân tại C (đpcm).}\)
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBD có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=8/3cm
c: Xét ΔCBD co
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C














