Question

Cho tam giác ABC vuông cân tại A, đường cao AH. Từ A kẻ đường thẳng song song với cạnh BC cắt đường thẳng kẻ từ B và song song với AH tại E

a) Chứng minh tứ giác AHBE là hình vuông

b) Đường thẳng song song với EH kẻ từ B cắt đường thẳng AH tại D. Chứng minh tứ giác ABDC là hình vuông 

Answer 1

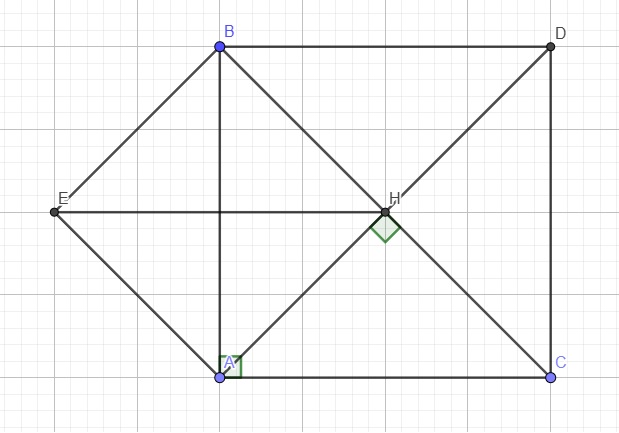
a.

Do AH là đường cao nên \(AH\perp BC\Rightarrow\widehat{AHB}=90^0\)

Theo giả thiết AE song song BC \(\Rightarrow AE\perp AH\) \(\Rightarrow\widehat{HAE}=90^0\)

Theo giả thiết BE song song AH \(\Rightarrow BE\perp BC\Rightarrow\widehat{HBE}=90^0\)

\(\Rightarrow AHBE\) là hình chữ nhật (tứ giác có 3 góc vuông)

Mặt khác ABC vuông cân tại A nên AH đồng thời là trung tuyến

\(\Rightarrow AH=\dfrac{1}{2}BC=BH\) (trung tuyến ứng với cạnh huyền)

\(\Rightarrow AHBE\) là hình vuông (hcn có 2 cạnh kề bằng nhau)

b.

Ta có: \(\left\{{}\begin{matrix}BD||EH\left(gt\right)\\BE||AH\left(gt\right)\Rightarrow BE||DH\end{matrix}\right.\)

\(\Rightarrow BDHE\) là hbh (tứ giác có 2 cặp cạnh đối song song)

\(\Rightarrow DH=BE\)

Mà AHBE là hình vuông \(\Rightarrow BE=AH\)

\(\Rightarrow DH=AH\Rightarrow H\) là trung điểm AD

\(\Rightarrow ABDC\) là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)

Lại có \(\widehat{A}=90^0\left(gt\right)\Rightarrow ABDC\) là hình chữ nhật (hbh có 1 góc vuông)

\(AB=AC\left(gt\right)\Rightarrow ABDC\) là hình vuông (hcn có 2 cạnh kề bằng nhau)

Answer 2