Các câu hỏi tương tự
Cho tam giác ABC, M là điểm thỏa mãn
|2\(\overrightarrow{MA}\) + \(\overrightarrow{MB}\)|. Tập hợp điểm M là:
A. Là đỉnh thứ tư của hình bình hành dựng trên hai cạnh AB, AC
B. Đường trung trực của đoạn thẳng cố định
C. Đường thẳng đi qua trung điểm của AB và song song với BC D. Là đường tròn có bán kính bằng BC
Cho hình bình hành ABCD tâm O. Xác định vị trí điểm M thỏa mãn \(\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{AM}\). Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và dựng điểm K sao cho \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\). Khi đó, điểm K trùng với
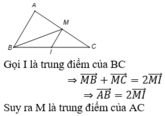
Cho I; J; K lần lượt là trung điểm của các cạnh AB; BC; CA của tam giác ABC. Giả sử M là điểm thỏa mãn điều kiện
M
A
→
+
2
M
B
→
+
M
C
→
0
→
. Khi đó vị trí điểm M là: A. M là giao điểm 2 đường chéo của hình bình hành BIKJ. B....
Đọc tiếp
Cho I; J; K lần lượt là trung điểm của các cạnh AB; BC; CA của tam giác ABC. Giả sử M là điểm thỏa mãn điều kiện M A → + 2 M B → + M C → = 0 → . Khi đó vị trí điểm M là:
A. M là giao điểm 2 đường chéo của hình bình hành BIKJ.
B.M là đỉnh thứ tư của hình bình hành AIKM.
C. M là trực tâm của tam giác ABC.
D.M là trọng tâm của tam giác IJK.
Cho tam giác ABC, gọi D là điểm trên cạnh BC sao cho vecto BD=2/3 vecto BC và I là trung điểm của AD. Gọi M là điểm thỏa mãn vecto AM=2/5 vecto AC. Chứng minh B,I,M thẳng hàng
Cho tam giác ABC, gọi D là điểm trên cạnh BC sao cho vecto BD=2/3 vecto BC và I là trung điểm của AD. Gọi M là điểm thỏa mãn vecto AM=2/5 vecto AC. Chứng minh B,I,M thẳng hàng
Cho tam giác ABC có M là trung điểm của trung tuyến AD, N là điểm thỏa mãn hệ thức: 3vecto AN=vectoAC
a) Chứng minh rằng 3 điểm B, M, N thẳng hàng.
b) Trên AB lấy điểm I sao cho vecto AI=2/3AB, trên AC lấy điểm J sao cho vecto AJ=2/5 vecto AC .
Chứng minh rằng 3 điểm I, M, J thẳng hàng.
giúp em làm phần b với ạ,,em cần gấp ạ
trong mặt phẳng tọa độ oxy, cho 3 điểm A (3;3) B (4;-2) C(-1;-1)
1. tính vecto AB và vecto BC từ đó suy ra A,B, C là ba đỉnh của một tam giác
2. Tìm tọa độ điểm M thỏa mãn vecto MA + 4MB - MC = 0
3. Cho hình bình hành ABCD. Gọi I là trung điểm cạnh bC và E là điểm xác định bởi vecto AE = 2/3AC. CMR: vecto DI = AB - 1/2AD và 3 điểm D, E, I thẳng hàng
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.A. AD BC . B. MQ PN . C. MN QP . D. AB DC .Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúngA. HA CD và AD CH .B....
Đọc tiếp
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.
A. AD BC . B. MQ PN . C. MN QP . D. AB DC .
Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng
A. HA CD và AD CH .
B. HA CD và DA HC .
C. HA CD và AD HC .
D. HA CD và AD HC và OB OD .
Câu 1: Cho ABCD là hình vuông cạnh bằng 1. Khi đó độ dài của AC bằng
A. 1. B. 2. C. 2. D. 3.
Câu 2: Cho tam giác ABC vuông tại C có cạnh AC cm BC cm 4 , 3 . Độ dài của vectơ AB là
A. 7 . cm B. 6 . cm C. 5 . cm D. 4 . cm
Câu 3: Cho hình vuông ABCD tâm O, cạnh 2a. Độ dài vectơ DO bằng
A. 2 2. a B. 2 . 2 a C. a 2. D. 2 2. a
Câu 4: Cho đoạn thẳng AB cm 10 , điểm C thỏa mãn AC CB . Độ dài vectơ AC là
A. 10 . cm B. 5 . cm C. 20 . cm D. 15 . c
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).a/ Tìm tọa độ trọng tâm G của tam giác ABC.b/ Tìm tọa độ điểm D để ABCD là hình bình hànhc/ Tìm tọa độ sao cho Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng:
Đọc tiếp
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).
a/ Tìm tọa độ trọng tâm G của tam giác ABC.
b/ Tìm tọa độ điểm D để ABCD là hình bình hành
c/ Tìm tọa độ ![]() sao cho
sao cho ![]()
Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng: 
Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của BC, CD; G là trọng tâm tam giác ABC.
a) Chứng minh AM + AN = 3/2 AC và GA +3GB+GC+GD=0
c) Gọi I là điểm thỏa mãn AI= 3/4AB. Phân tích IN ; IG theo hai vec tơ BA và BC
Chứng minh 3 điểm N;G;I thẳng hàng.