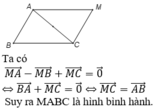Các câu hỏi tương tự
Trong các mệnh đề sau a. Nếu tam giác ABC thỏa mãn AB2 + AC2 BC2 thì tam giác ABC vuông tại B. b. Nếu một phương trình bậc hai có biệt thức không âm thì nó có nghiệm. c. Tam giác ABC là tam giác đều khi và chỉ khi nó thỏa mãn đồng thời hai điều kiện AB AC và góc A 600. d. Hình thang cân có một trục đối xứng. Các mệnh đề đúng là: A. a, c. B. a, b, c. C. b, c. D. b, c, d.
Đọc tiếp
Trong các mệnh đề sau
a. Nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại B.
b. Nếu một phương trình bậc hai có biệt thức không âm thì nó có nghiệm.
c. Tam giác ABC là tam giác đều khi và chỉ khi nó thỏa mãn đồng thời hai điều kiện AB = AC và góc A = 600.
d. Hình thang cân có một trục đối xứng.
Các mệnh đề đúng là:
A. a, c.
B. a, b, c.
C. b, c.
D. b, c, d.
Cho hình vuông ABCD với P là giao điểm hai đường chéo BD và AC, M là giao điểm thỏa mãn vecto MO= vecto DC + vecto OB. Mệnh đề nào dưới đây đúng A. M đối xứng với C qua B B. M là trung điểm của AD C. M đối xứng với V qua D D. M đối xứng với A qua B
Gọi S = \(m^2_a+m^2_b+m^2_c\) là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng?
A. S = \(\dfrac{3}{4}\left(a^2+b^2+c^2\right)\)
B. S = \(a^2+b^2+c^2\)
D. S = 3\(\left(a^2+b^2+c^2\right)\)
C. S = \(\dfrac{3}{2}\left(a^2+b^2+c^2\right)\)
Cho tam giác ABC. Điểm M thỏa mãn điều kiện
M
A
→
-
M
B
→
+
M
C
→
0
→
thì điều kiện cần và đủ là A. M là điểm sao cho tứ giác ABMC là hình bình hành B. M là trọng tâm tam giác ABC C. M là điểm sao cho tứ giác BAMC là hình bình hành D. M...
Đọc tiếp
Cho tam giác ABC. Điểm M thỏa mãn điều kiện M A → - M B → + M C → = 0 → thì điều kiện cần và đủ là
A. M là điểm sao cho tứ giác ABMC là hình bình hành
B. M là trọng tâm tam giác ABC
C. M là điểm sao cho tứ giác BAMC là hình bình hành
D. M thuộc trung trực của AB
cho tam giác abc và 2 điểm M,N thỏa mãn điều kiện MA+3MC=0,NA+2NB+3NC=0,chưmgs minh b,m,n thẳng hàng
Cho tam giác đều ABC và điểm I thỏa mãn
I
A
→
2
I
B
→
.
Mệnh đề nào sau đây đúng? A.
C
I
→
C
A
→
−
2
...
Đọc tiếp
Cho tam giác đều ABC và điểm I thỏa mãn I A → = 2 I B → . Mệnh đề nào sau đây đúng?
A. C I → = C A → − 2 C B → 3 .
B. C I → = C A → + 2 C B → 3 .
C. C I → = − C A → + 2 C B → .
D. C I → = C A → + 2 C B → − 3 .
Cho tam giác ABC đều.Gọi D là điểm đối xứng của C qua AB.Vẽ đường tròn tâm D qua A, B và M là điểm bất kì trên đường tròn đó
M
≠
A
,
M
≠
B
Khẳng định nào sau đây đúng? A. Độ dài MA; MB; MC là độ dài ba cạnh của một tam giác vuông. B. MA, MB, MC là ba cạnh của 1 tam giác vuông. C. MA MB MC D. MC MB MA
Đọc tiếp
Cho tam giác ABC đều.Gọi D là điểm đối xứng của C qua AB.Vẽ đường tròn tâm D qua A, B và M là điểm bất kì trên đường tròn đó M ≠ A , M ≠ B Khẳng định nào sau đây đúng?
A. Độ dài MA; MB; MC là độ dài ba cạnh của một tam giác vuông.
B. MA, MB, MC là ba cạnh của 1 tam giác vuông.
C. MA= MB= MC
D. MC> MB> MA
Cho tam giác ABC thỏa mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng?
A. CosB + Cos C = 2 Cos A B. Sin B + Sin C = 2 Sin A
C. Sin B + Sin C = \(\dfrac{1}{2}SinA\) D. Sin B + Sin C = 2 Sin A
Cho tam giác ABC có M thỏa mãn điều kiện
M
A
→
+
M
B
→
+
M
C
→
0
→
. Xác định vị trí điểm M A. M là điểm thứ tư của hình bình hành ACBM B.M là trung điểm của đoạn thẳng AB C.M trùng...
Đọc tiếp
Cho tam giác ABC có M thỏa mãn điều kiện M A → + M B → + M C → = 0 → . Xác định vị trí điểm M
A. M là điểm thứ tư của hình bình hành ACBM
B.M là trung điểm của đoạn thẳng AB
C.M trùng C
D.M là trọng tâm tam giác ABC