Các câu hỏi tương tự
cho tam giác ABC nhọn , AB<AC nội tiếp đường tròn (O). Các đường cao BD và CE của tam giác ABC cắt nhau tại H. Gọi K là giao điểm của DE và CB.
a)CMR: Tứ giác BCDE nội tiếp
b) C/m : KB.KC=KE.KD
c) Gọi M là trung điểm của BC , AK cắt đường tròn (O) tại điểm thứ 2 N . C/m : 3 điểm M,H,N thẳng hàng
cho tam giác abc có ba góc nhọn (ab<ac) nội tiếp đường tròn o .Các đường cao bd ce của tam giác cắt nhau tại h a) chúng minh bedc nội tiếp b)chứng minh ae.ab=ad.ac c)đường tròn đường kính ah cắt đường tròn (o,r) tại f. chứng minh de af bc đồng quy tại 1 điểm MÌNH CẦN GẤP PHẦN C
Cho tam giác ABC nhọn nội tiếp đường tròn (O).
Các đường cao BD, CE của tam giác ABC cắt nhau tại H
và cắt đường tròn (O) lần lượt tại M và N. Chứng minh:
a. Các tứ giác ADHE, BEDC nội tiếp
b. DE/MN
c. OA.LDE
cho tam giác abc nhọn (ab ac) nội tiếp đường tròn hai đường cao BD và CE cắt nhau tại h đường ah cắc bc và đường trong tâm o lần lượt tại F và K
a) chứng minh tg BEDC nội tiếp
b) gọi I là hình chiếu của d lên AB c/m BD^2 = BI.BA
c) Gọi J là giao điểm của KD và đường tròn tâm o c/m góc BJK = góc BDE
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn O. Các đường cao AD,BE,CF cắt nhau tại H.Gọi I là trung điểm của BC.Nối A với I cắt OH tại Ga) tg BCEF nội tiếpb) Tính EF nếu BÂC 60 độ và BC20cmc) C/m G là trọng tâm tam giác ABCd) c/m rằng khi A chuyển động trên cung lớn BC sao cho tam giác BAC có 2 góc nhọn thì đường tòn ngoại tiếp tam giác DEF luôn đi qua 1 điểm cố định
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn O. Các đường cao AD,BE,CF cắt nhau tại H.Gọi I là trung điểm của BC.Nối A với I cắt OH tại G
a) tg BCEF nội tiếp
b) Tính EF nếu BÂC =60 độ và BC=20cm
c) C/m G là trọng tâm tam giác ABC
d) c/m rằng khi A chuyển động trên cung lớn BC sao cho tam giác BAC có 2 góc nhọn thì đường tòn ngoại tiếp tam giác DEF luôn đi qua 1 điểm cố định
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn O. Các đường cao AD,BE,CF cắt nhau tại H.Gọi I là trung điểm của BC.Nối A với I cắt OH tại Ga)tg BCEF nội tiếpb) Tính EF nếu BÂC 60 độ và BC20cmc) C/m G là trọng tâm tam giác ABCd) c/m rằng khi A chuyển động trên cung lớn BC sao cho tam giác BAC có 2 góc nhọn thì đường tòn ngoại tiếp tam giác DEF luôn đi qua 1 điểm cố định
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn O. Các đường cao AD,BE,CF cắt nhau tại H.Gọi I là trung điểm của BC.Nối A với I cắt OH tại G
a)tg BCEF nội tiếp
b) Tính EF nếu BÂC =60 độ và BC=20cm
c) C/m G là trọng tâm tam giác ABC
d) c/m rằng khi A chuyển động trên cung lớn BC sao cho tam giác BAC có 2 góc nhọn thì đường tòn ngoại tiếp tam giác DEF luôn đi qua 1 điểm cố định
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O, 2 đường cao BD,CE cắt nhau tại H.
a) Cm: ADHE là tứ giác nội tiếp (GIẢI XONG RỒI)
b) Tia AH cắt đường tròn tại I , C/m : góc BIC = góc BHC (GIẢI XONG RỒI)
c) Đường thẳng DE cắt 2 cung nhỏ AB, AC theo thứ tự tại M, N . C/m : tam giác AMN cân (GIẢI GIÙM EM CÂU NÀY VỚI)
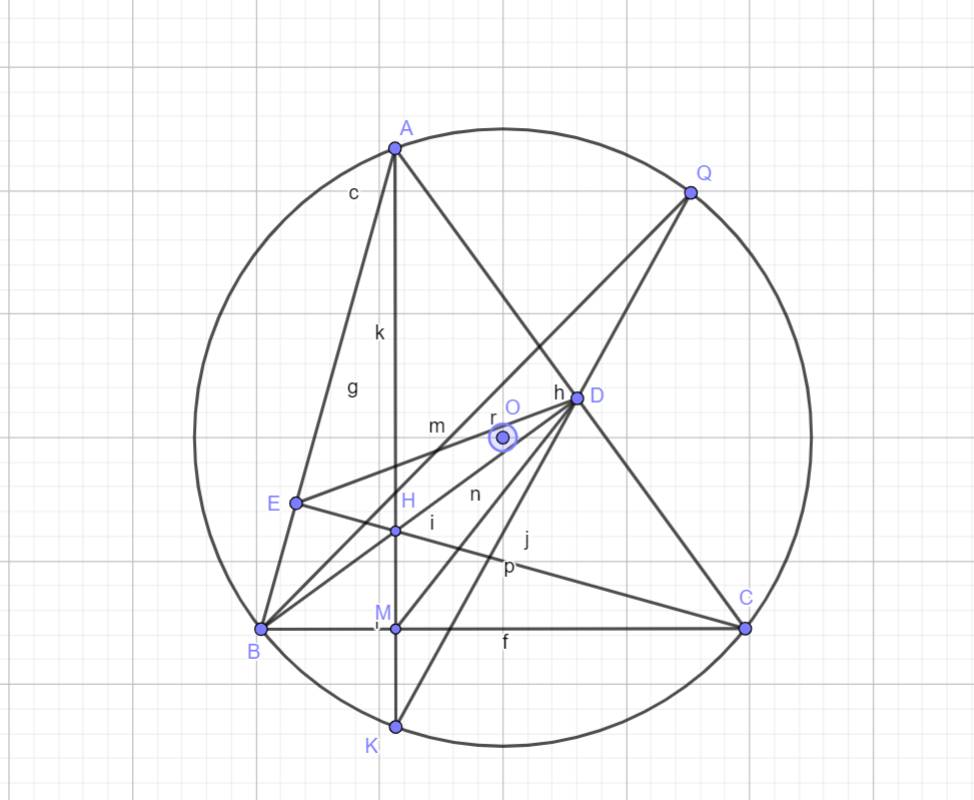
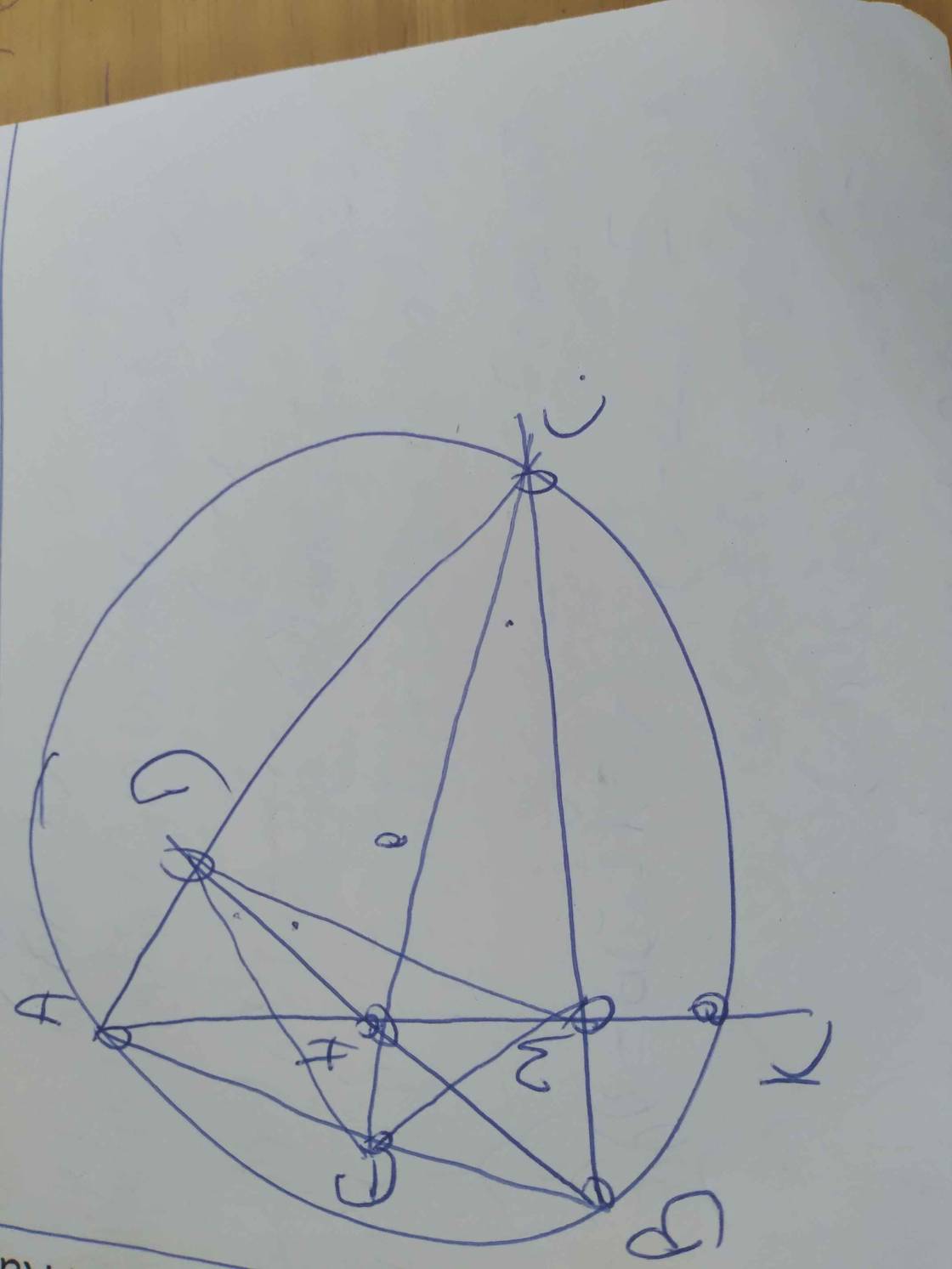
Cho tam giác nhọn ABC nội tiếp (O). Hai đường cao BD và CE cắt nhau tại H. Tia BD cắt (O) tại M, CE cắt (O) tại N. Đường tròn đường kính AH cắt (O) tại điểm thứ 2 là K (K khác A). Tia KH cắt (O) tại điểm Q. Chứng minh: BHCQ là hình bình hành.
Giúp em câu (c) với câu (d) , please !
Cho tam giác ABC nhọn (AB<AC) nội tiếp (O). Gọi I là trung điểm BC. Tiếp tuyến tại C của (O) cắt OI tại M. Đường thẳng MA cắt (O) tại D.
a) C/m MB là tiếp tuyến (O) và MBOC nội tiếp
b) C/m Tam giác MDI đồng dạng tam giác MOA
c) C/m CI/CA=DB/DA
d) Đường thẳng qua I vuông góc với OC cắt AC tại F. C,m BF // CD
A B C D E H D E Cho tam giác ABC nội tiếp O .BD, CE là 2 đường cao. BD cắt CE tại H và cắt O tại lần lượt D ,E .Chứng minh a BEDC nội tiếpb DE D E c OA vuông góc DEd BC cố định. Chứng minh khi A di động trên cung lớn BC sao cho tam giác ABC luôn là tam giác nhọn thì bán kính đtròn ngoại tiếp tam giác ADE ko đổi.