Các câu hỏi tương tự
1. Cho tam giác abc nhọn nội tiếp đường tròn tâm O. Hai đường cao BE, CF của tam giác ABC cắt nhau tại H
a) Chứng minh tứ giác BFEC nội tiếp đường tròn
b) Chứng minh rằng AF.AB=AE.AC
c) Kẻ đường kính AD của đường tròn tâm O. Chứng minh tứ giác BHCD là hình bình hành
Cho tam giác ABC có ba góc nhọn (AB<AC) nội tiếp đường tròn (O). Vẽ ba đường cao AD;BE và CF cắt nhau tại H.
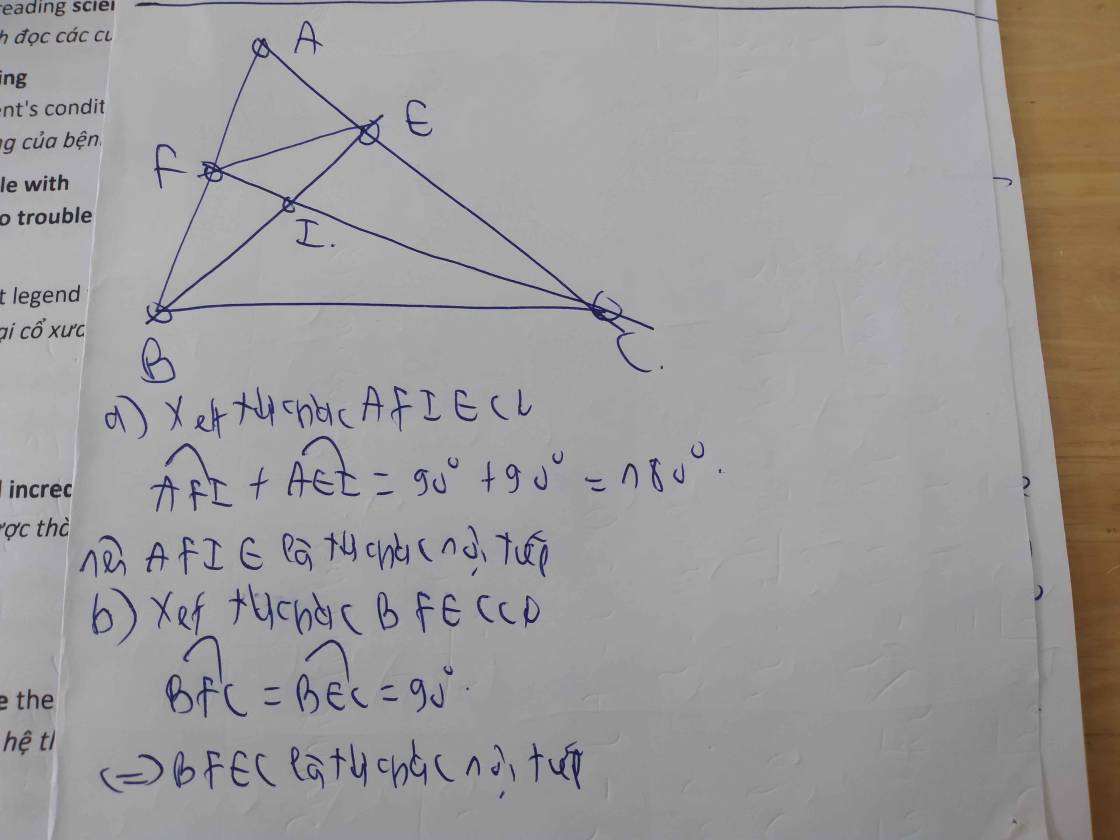
a) Chứng minh tứ giác AFHE và tứ giác BFEC là các tứ giác nội tiếp đường tròn
b) Đường thẳng EF cắt BC tại I. Chứng minh IE.IF=IB.IC
c) AI cắt đường tròn (O) tại K. Gọi M là trung điểm BC. Chứng minh ba điểm K,H,M thẳng hàng
Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O;R). Vẽ đường cao BE và CF cắt nhau tại H.
a) Chứng minh: Tứ giác AEHF nội tiếp đường tròn.
b) Chứng minh: AB . CE = CH . BE c) Chứng minh: OA ⊥ EF
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R) (AB
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R) (AB<AC) 3 đường cao AD,BE,CF cắt nhau tại H
a,CM tứ giác BFEC nội tiếp và xác định tâm I
b,Đường thẳng EF cắt đường thẳng BC tại K . CM KF.KE=KB.KC
c,AK cắt (O) tại M. CM MFEA nội tiếp
jup mình vs ạ
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF 2
Đọc tiếp
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF =2
Cho tam giác ABC nhọn nối tiếp đg tròn (O;R). Các đường cao AD,BE,CF cắt nhau tại H
a, chứng minh các tứ giác BFEC VÀ CEHD nội tiếp
b, chứng minh OA ⊥ EF
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Hai đường cao BD, CE của tam giác ABC cắt nhau tại H. a) Chứng minh tứ giác BFEC nội tiếp được một đường tròn. b) Kẻ đường kính AD của đường tròn (O). Tứ giác BFCD là hình gì? Vì sao? c) Gọi M là trung điểm của BC. Chứng minh AH = 2OM. d) Chứng minh OA | EF
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H và lần lượt cắt đường tròn tại M, N, P. Chứng minh rằng:
1) Tứ giác BFEC và AEDB nội tiếp.
2) AE.AC = AF.AB.
3) Chứng minh H là tâm đường tròn nội tiếp tam giác EFD.
Cho tam giác ABC nhọn nội tiếp (O) . Các đường cao AD, BE , và CF cắt nhau tại H . Đường thẳng EF cắt đường tròn ở I và K a) chứng minh : Tứ giác CDHE nội tiếp đường trònb) Chứng minh : AH . AD = AF . ABc) Kẻ tiếp tuyến Ax, chứng minh: BCEF nội tiếp. Từ đó chứng minh : Ax // IK
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O(AB<AC), có ba đường cao AD, BE, CF cắt nhau tại H ( D thuộc BC, E thuộc AC, F thuộc AB)
a) Chứng minh tứ giác BFEC và tứ giác BFHD là các tứ giác nội tiếp
b) Vẽ đường kính AK của (O). Chứng minh AB.AC=AD.AK