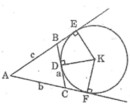
Ta có: C F = A F - A C = a + b + c 2 - b = a + c - b 2
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC a, AC b, AB c. Chứng minh rằng:
B
E
a
+
b
-
c
2
Đọc tiếp
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC = a, AC = b, AB = c. Chứng minh rằng: B E = a + b - c 2
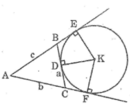
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC a, AC b, AB c. Chứng minh rằng:
A
E
A
F
a
+
b
+
c
2
Đọc tiếp
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC = a, AC = b, AB = c. Chứng minh rằng: A E = A F = a + b + c 2

cho đường tròn [ I;r] nội tiếp tam giác ABC tiếp xúc với các cạnh AB và AC lần lượt tại D và E. đường tròn [ K;ra] là đường tròn bàng tiếp trong góc A tiếp xúc với BC tại F tiếp xúc phần kéo dài của 2 cạnh AB; AC lần lượt tại M;N. cho AB=c; BC=a; AC=b; nửa chu vi tam giác ABC=p. chứng minh
a: AD=AE=p-a
b: AM=AN=p
c: diện tích tam giác ABC= p.r
d: diện tích tam giác ABC=[p-a].ra
Bài 3: Cho tam giác ABC. Gọi (P), (Q), (R) theo thứ tự là các đường tròn bàng tiếp trong các góc A, B, C. Gọi tiếp điểm của (Q), (R) trên đường thẳng BC theo thứ tự E, F. Chứng minh rằng CE = BF. Gọi H, I, K theo thứ tự là tiếp điểm của các đường tròn (P), (Q), (R) với các cạnh BC, AC, AB. Nếu AH = BI = CK thì tam giác ABC là tam giác gì?
Một đường tròn tiếp xúc với hai cạnh của một góc vuông đỉnh A tại hai điểm B và C. Kẻ một tiếp tuyến (d) với đường tròn đã cho cắt các đoạn thẳng AB và AC theo thứ tự E và F. Chứng minh rằng:
\(\dfrac{AB+AC}{3}< EB+FC< \dfrac{AB+AC}{2}\)
Cho tam giác ABC nhọn (ABAC), kẻ phân giác AD của góc BAC và đường trung tuyến AM (M,D thuộc BC). Vẽ 2 đường tròn ngoại tiếp các tam giác ABC và ADM, 2 đường tròn này cắt nhau tại điểm thứ 2 là I, đường tròn ngoại tiếp tam giác ADM cắt 2 cạnh AB và AC theo thứ tự tại E và F. Tia AD cắt đường tròn ngoại tiếp tam giác ABC tại J.a, Chứng minh 3 điểm I; M; J thẳng hàng.b, Gọi K là trung điểm È, tia MK cắt AC và tia BA theo thứ tự tại P và Q. Chứng minh tam giác PAQ cân
Đọc tiếp
Cho tam giác ABC nhọn (AB<AC), kẻ phân giác AD của góc BAC và đường trung tuyến AM (M,D thuộc BC). Vẽ 2 đường tròn ngoại tiếp các tam giác ABC và ADM, 2 đường tròn này cắt nhau tại điểm thứ 2 là I, đường tròn ngoại tiếp tam giác ADM cắt 2 cạnh AB và AC theo thứ tự tại E và F. Tia AD cắt đường tròn ngoại tiếp tam giác ABC tại J.
a, Chứng minh 3 điểm I; M; J thẳng hàng.
b, Gọi K là trung điểm È, tia MK cắt AC và tia BA theo thứ tự tại P và Q. Chứng minh tam giác PAQ cân
Cho đường tròn (O), từ điểm A nằm ngoài đường tròn, kẻ 2 tiếp tuyến AB, AC ( B, C là các tiếp điểm. OA cắt BC tại Ea) Chứng minh tứ giác ABOC nội tiếpb) BC⊥OA;BA.BEAE.BOc) GỌi I là trung điểm BE, đường thẳng qua I và vuông góc với OI cắt các tia AB, AC theo thứ tự tại D và F. Chứng minh:^IDO^BCOvà tam giác DOF cân tại Od) Chứng minh F là trung điểm AC
Đọc tiếp
Cho đường tròn (O), từ điểm A nằm ngoài đường tròn, kẻ 2 tiếp tuyến AB, AC ( B, C là các tiếp điểm. OA cắt BC tại E
a) Chứng minh tứ giác ABOC nội tiếp
b) BC⊥OA;BA.BE=AE.BO
c) GỌi I là trung điểm BE, đường thẳng qua I và vuông góc với OI cắt các tia AB, AC theo thứ tự tại D và F. Chứng minh:^IDO=^BCOvà tam giác DOF cân tại O
d) Chứng minh F là trung điểm AC
Cho tam giác ABC có độ dài ba cạnh AB c, AC b, BA a và p là nửa chu vi của tam giác. Đường tròn tâm I nội tiếp tam giác lần lượt tiếp xúc với BC, AC và AB tại D, E và Fa, Chứng minh (I) có bán kính r (p – a)tan
B
A
C
^
2
b, Với
B
A
C
^...
Đọc tiếp
Cho tam giác ABC có độ dài ba cạnh AB = c, AC = b, BA = a và p là nửa chu vi của tam giác. Đường tròn tâm I nội tiếp tam giác lần lượt tiếp xúc với BC, AC và AB tại D, E và F
a, Chứng minh (I) có bán kính r = (p – a)tan B A C ^ 2
b, Với B A C ^ = α, tìm số đo của góc EDF theo α
c, Gọi H, K lần lượt là hình chiếu của B,C trên EF. Chứng minh: ∆BHF:∆CKE
d, Kẻ DP vuông góc vói EF tại P. Chứng minh: ∆FPB:∆CEP và PD là tia phân giác của góc B P C ^
Cho tam giác ABC. D là tiếp điểm của đường tròn bàng tiếp góc A với BC.
a) Chứng minh rằng AB + BD = AC +CD.
b) Chứng minh rằng đường tròn bàng tiếp góc A của hai tam giác ADB và ADC tiếp xúc nhau.