Question

cho tam giác abc có hai đường trung tuyến BM=CN.C/m abc cân

Answer 1

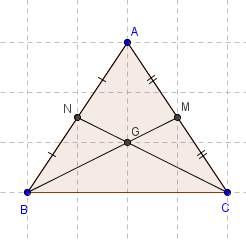
Gọi G là giao điểm của BM và CN

\(\Rightarrow\) G là trọng tâm của \(\Delta ABC\)
\(\Rightarrow\) GB = \(\dfrac{2}{3}\).BM 
GC = \(\dfrac{2}{3}\).CN 
Mà BM = CN (gt)

\(\Rightarrow\) GB = GC 
\(\Rightarrow\Delta GBC\) cân tại G 
\(\Rightarrow\widehat{MBC}=\widehat{NCB}\)
Xét ΔBMC và ΔCNB có: 
BM = CN (gt)
\(\widehat{MBC}=\widehat{NCB}\)  (cmt)
BC là cạnh chung 
\(\Rightarrow\) ΔBMC = ΔCNB (c - g - c) 
\(\Rightarrow\) \(\widehat{MCB}=\widehat{NBC}\)  (hai góc tương ứng)
\(\Rightarrow\widehat{ACB}=\widehat{ABC}\)
\(\Rightarrow\) ΔABC cân tại A

Answer 2

Gọi giao của BM và CN là G

=>G là trọng tâm của ΔABC

=>GB=GC

=>ΔGBC cân tại G

=>góc GBC=góc GCB

Xet ΔNBC và ΔMCB có

NC=MB

góc NCB=góc MBC

CB chung

=>ΔNBC=ΔMCB

=>góc ABC=góc ACB

=>ΔBAC cân tại A