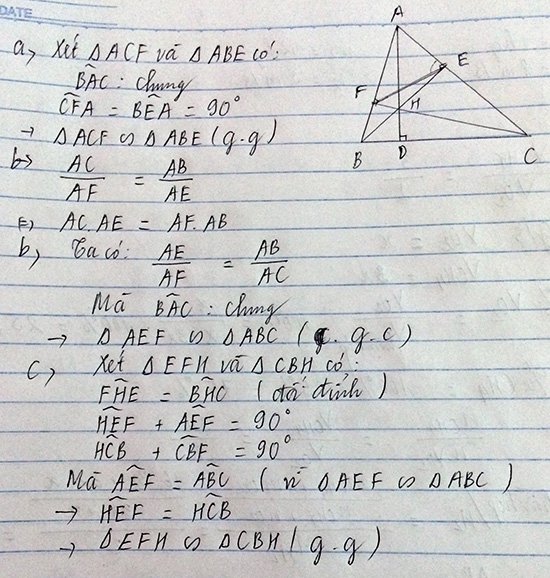Các câu hỏi tương tự
Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:
a/ AE.AC = AF.AB
b/ △AFE∼△ACB
c/ △FHE∼△BHC
d/ BF.BA+CF.CA=BC2
Cho tam giác ABC có 3 góc nhọn ( AB<AC ), các đường cao AD, BE, CF cắt nhau tại H.
a) CM : Tam giác ABE đồng dạng tam giác ACF và AE.AC = AF.AB
b) CM : Tam giác AEF đồng dạng tam giác ABC và góc AEF = góc ABC
c) Gọi I là trung điểm của AH, M là trung điểm của BC. CM : MI vuông góc EF
Bài 7: Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
a) CMR: AE . AC = AF . AB
b) CMR: ΔAFE đồng dạng ΔACB
c) CMR: ΔFHE đồng dạng ΔBHC
d ) CMR: BF . BA + CE . CA = BC2
Cho tam giác ABC có các góc đều nhọn, các đường cao AD, BE, CF cắt nhau tại H. CMR: AH/HD+BH/HE+CH/FH>=6.
) Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau tại H. 1) Chứng minh rằng: AE.AC AF.AB2) Chứng minh rằng tam giác AFE đồng dạng tam giác ACB3) Chứng minh rằng tam giác FHE đồng dạng tam giác BHC4) Chứng minh rằngBF.BA+CE.CA BC2
Đọc tiếp
) Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau tại H.
1) Chứng minh rằng: AE.AC = AF.AB
2) Chứng minh rằng tam giác AFE đồng dạng tam giác ACB
3) Chứng minh rằng tam giác FHE đồng dạng tam giác BHC
4) Chứng minh rằngBF.BA+CE.CA = BC2
Cho tam giác ABC (các góc đều nhọn) các đường cao AD, BE và CF cắt nhau tại H. Gọi M là trung điểm của BC. Đường thẳng qua H vuông góc với MH cắt AB tại P, cắt AC tại Q Cmr a) tam giác AHP đồng dạng với tam giác CMH, tam giác QHA đồng dạng với tam giác HMB b) HP/AH =MH/CM c) HP=HQ
cho tam giác ABC nhọn các đường cao AD,BE,CF cắt nhau tại H . hãy chứng minh
1) AE.AC=AF.AB
2) tam giác AFE đồng dạng tam giác ACB
giúp mik nha mn
Cho tam giác ABC nhọn có các đường cao AD , BE , CF cắt nhau tại H
CMR : a, AF. AB = AE.AC
b,BH.BE=BD.BC
c, BF.BA+CE.CA=BC2
cho tam giác abc có 3 góc nhọn, hai đường cao BE, CF, AH cắt nhau tại H: a)AE.AC=AF.AB . b) CMR: Tam giác(tg)AEF~tgABC. c)CMR: tam giác AEF đồng dạng tam giác CED từ đó suy ra: Tia EH là phân giác góc FED