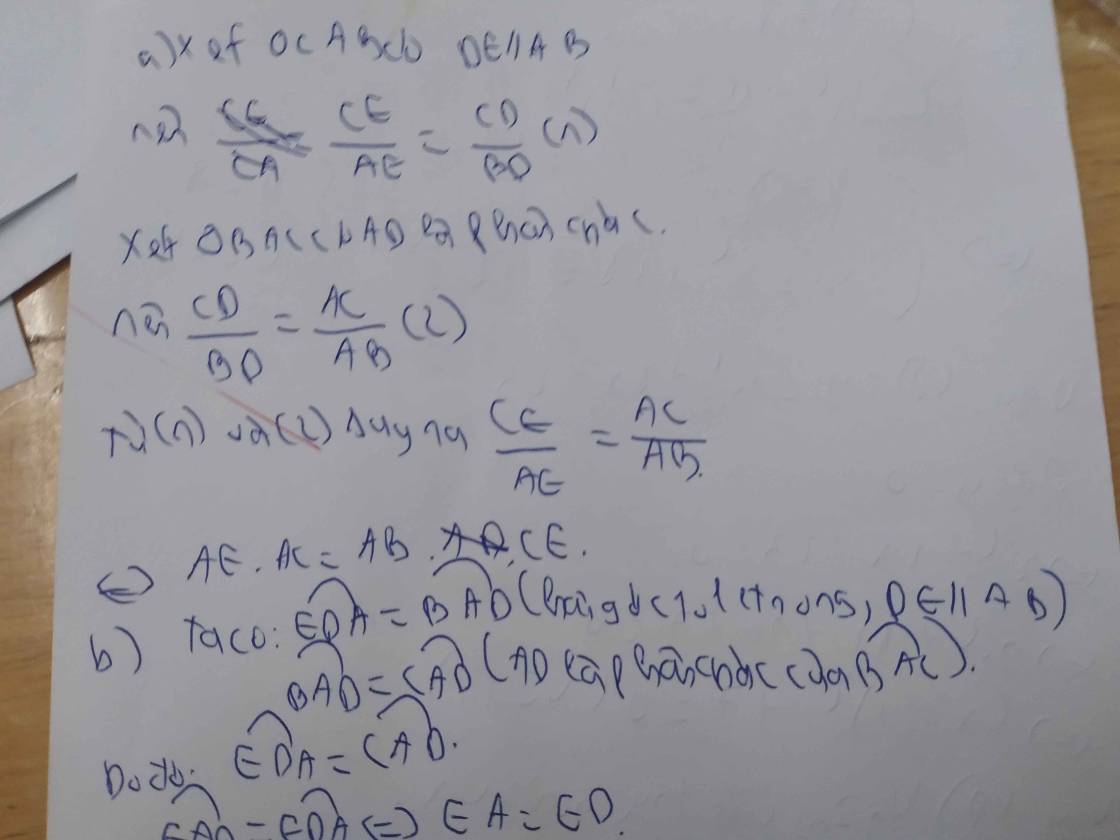Các câu hỏi tương tự
MÌNH ĐANG CẦN GẤP
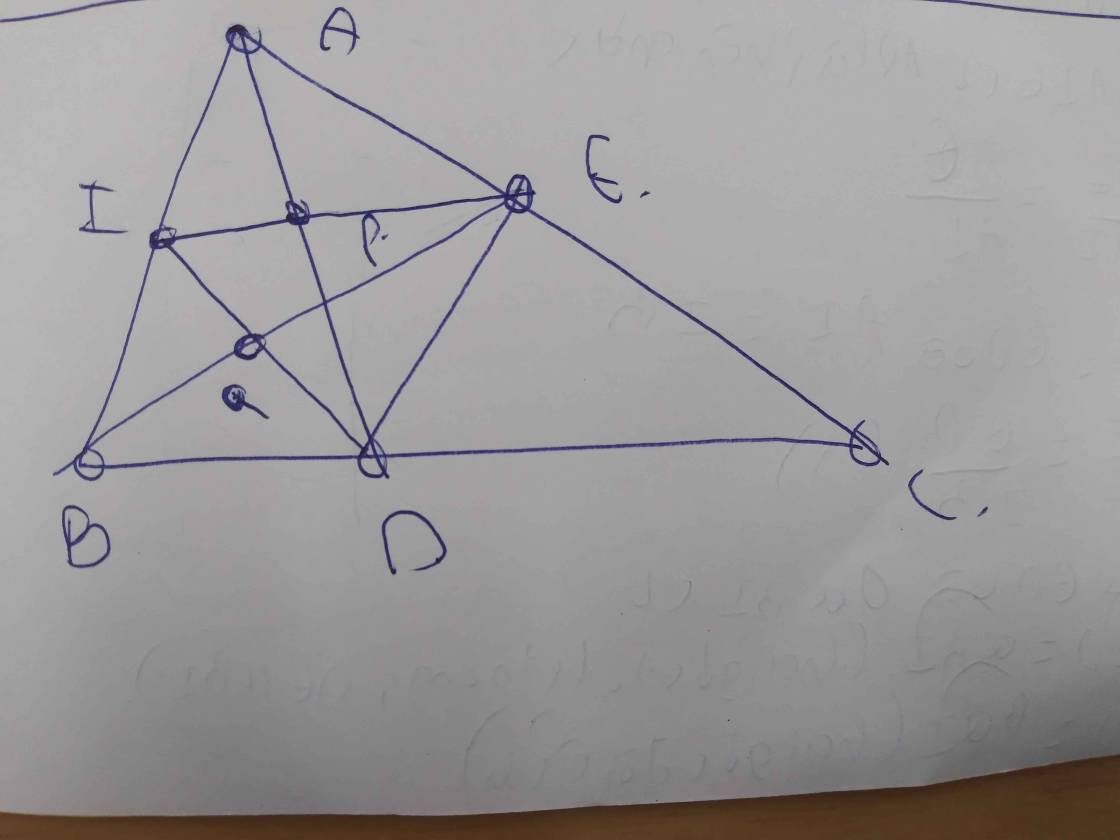
Cho tam giác ABC có AD là đường phân giác. a) Cho AC= 16cm, BD=6cm, DC=8cm. Tính độ dài đoạn thẳng AB. b) Qua D kẻ đường thẳng song song với AB, cắt AC tại E. Chứng minh AC.EA=AB.EC c) Gọi I là trung điểm của AB, AD cắt EI tại P, BE cắt ID tại Q. Chứng minh rằng \(\dfrac{PE}{PI}=\dfrac{QD}{QI}\)
Cho tam giác ABC ( AB<AC) , tia phân giác của góc A cắt cạnh BC tại D . Gọi M là trung điểm của cạnh BC, qua M kẻ đường thẳng // với AD, đường thẳng này cắt tia đối của AB tại E và cắt cạnh AC tại F. C/M: BE=FC
Bài 1: Cho tam giác ABC, trên cạnh AB lấy 2 điểm D và F sao cho AD DF FB. Các trung tuyến AE, BG của tam giác ABC lần lượt cắt CD, CF tại H và K.a) CMR: GH, EK, AB cắt nhau tại 1 điểmb) CMR: AB 4HKBài 2: Cho tam giác ABC có BD và CE là phân giác, cắt nhau tại I. Gọi S là trung điểm BC, biết BI 2IS.a) CMR: tam giác ABC vuôngb) CMR: ID / IB CD / CBBài 3: Cho tam giác ABC vuông cân tại A. Trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD AE. Qua A và D, kẻ các đường thẳng vuông góc v...
Đọc tiếp
Bài 1: Cho tam giác ABC, trên cạnh AB lấy 2 điểm D và F sao cho AD = DF = FB. Các trung tuyến AE, BG của tam giác ABC lần lượt cắt CD, CF tại H và K.
a) CMR: GH, EK, AB cắt nhau tại 1 điểm
b) CMR: AB = 4HK
Bài 2: Cho tam giác ABC có BD và CE là phân giác, cắt nhau tại I. Gọi S là trung điểm BC, biết BI = 2IS.
a) CMR: tam giác ABC vuông
b) CMR: ID / IB = CD / CB
Bài 3: Cho tam giác ABC vuông cân tại A. Trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD = AE. Qua A và D, kẻ các đường thẳng vuông góc với BE cắt BC thứ tự tại S và T. CMR: S là trung điểm của TC
Cho tam giác ABC, phân giác AD, qua D kẻ đường thẳng song song với AB cắt AC tại E. Qua E kẻ đường thẳng song song với BC cắt AB tại Fa) Chứng minh AEBFb) Kẻ phân giác ngoài tại A của tam giác ABC cắt DE tại G. Chứng minh rằng E là trung điểm của DGc) Đường thẳng vuông góc với AD tại D cắt AB, AC lần lượt tại H, K. Chứng minh AH2FBd) Từ E kẻ đường thẳng song song với DK cắt AD tại I.Chứng minh H, I, G thẳng hàng
Đọc tiếp
Cho tam giác ABC, phân giác AD, qua D kẻ đường thẳng song song với AB cắt AC tại E. Qua E kẻ đường thẳng song song với BC cắt AB tại F
a) Chứng minh AE=BF
b) Kẻ phân giác ngoài tại A của tam giác ABC cắt DE tại G. Chứng minh rằng E là trung điểm của DG
c) Đường thẳng vuông góc với AD tại D cắt AB, AC lần lượt tại H, K. Chứng minh AH=2FB
d) Từ E kẻ đường thẳng song song với DK cắt AD tại I.Chứng minh H, I, G thẳng hàng
Cho tam giác ABC nhọn có AB > AC. Các đường cao AD,BE, CF cắt tại H.
a) chứng minh rằng ∆AFH~∆ADB
b) ∆ AFE~∆ABC và EH là tia phân giác của góc FED
c) gọi I là trung điểm của BC qua H kẻ đường thẳng vuông góc với HI đường thẳng này cắt AB tại M, cắt AC tại N . Chứng minh ∆ IMN cân
Cho tam giác ABC (AB<AC). Đường phân giác AD của góc A cắt cạnh BC ở D, từ trung điểm M của BC kẻ đường thẳng // với AD cắt AC tại F và cắt đường thẳng AB tại E. Chứng minh BE = CF.
Cho tam giác ABC (AB<AC). Đường phân giác AD của góc A cắt cạnh BC ở D, từ trung điểm M của BC kẻ đường thẳng // với AD cắt AC tại F và cắt đường thẳng AB tại E. Chứng minh BE = CF.
1, Cho tam giác ABC có I là trung điểm của cạnh BC. Qua I kẻ đường thẳng d cắt AB,AC lần lượt tại M và N . Kẻ dường thẳng d' cắt AC,AB lần lượt tại E,F . CMR : IE=IF
2, cho hình thoi ABCD có góc B bằng 60 độ . Một đường thẳng đi qua D cắt đường kéo dài các cạnh AB,BC lần lượt tại E và F. Gọi M là giao điểm của AF, CE . Chứng minh rằng : AD^2 = AM.AF
Cho tam giác ABC có AD là phân giác của góc BAC ( D thuộc BC ) . TỪ D kẻ các đường thẳng song song vói AB và AC , chúng cắt AC , AB lần lượt tại E và F.a) CM : tứ giác AEDF là hình thoi b) Trên tia AB lấy G sao cho F là trung điểm của AG . Cm : tứ giác EFGD là hình bình hành c) Gọi I là điểm đối xứng của D qua F , tia IA cắt DE tại K . Gọi O là giao điểm của AD và EF . Cm G đối xúng với K qua O
Đọc tiếp
Cho tam giác ABC có AD là phân giác của góc BAC ( D thuộc BC ) . TỪ D kẻ các đường thẳng song song vói AB và AC , chúng cắt AC , AB lần lượt tại E và F.
a) CM : tứ giác AEDF là hình thoi
b) Trên tia AB lấy G sao cho F là trung điểm của AG . Cm : tứ giác EFGD là hình bình hành
c) Gọi I là điểm đối xứng của D qua F , tia IA cắt DE tại K . Gọi O là giao điểm của AD và EF . Cm G đối xúng với K qua O