góc B=góc C=(180-120)/2=30 độ
BC/sinA=AC/sinB=AB/sinC
=>BC/sin120=a/sin30=2a
=>\(BC=a\sqrt{3}\)
\(BD=\dfrac{2\cdot a\sqrt{3}\cdot a}{a\sqrt{3}+a}\cdot cos15=\dfrac{\sqrt{6}}{2}a\)
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Gọi M là một điểm trên cạnh BC và D là chân đường phân giác trong góc A. Tính độ dài vecto MD khi độ dài vecto AM nhỏ nhất
Cho tam giác ABC có AB =5a, BC=8a, góc ABC=60 , gọi M là trung điểm của BC. Tính theo a độ dài đoạn AM và bán kính đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC có góc A nhọn và AB = 3, AC=5, Sin A = 3/5. Gọi G là trọng tâm tam giác ABC và O là tâm đường tròn ngoại tiếp tam giác ABC
Tính độ dài đoạn thẳng OG
cho tam giác ABC gọi D là chân đường phân giác trong góc B và E là trung điểm BD. đường thẳng qua A song song với BD cắt CE tại F.Cho B (5;1), F(4;3) và điểm A thuộc đường thẳng (d) x+2y-18=0. tính khoảng cách từ gốc tọa độ O đến BC
cho tam giác ABC gọi D là chân đường phân giác trong góc B và E là trung điểm BD. đường thẳng qua A song song với BD cắt CE tại F.Cho B (5;1), F(4;3) và điểm A thuộc đường thẳng (d) x+2y-18=0. tính khoảng cách từ gốc tọa độ O đến BC
Tính độ dài đường trung tuyến
Cho tam giác ABC, có cạnh BC=a, AC=b, AB =c. Gọi ma , mb , mc lần lượt là độ dài trung tuyến từ đỉnh A, B, C của tam giác. Hãy tính ma , mb , mc theo a, b, c.
Cho tam giác ABC với AB= 5 và AC=1. Tính toạ độ điểm D là của chân đường phân giác trong góc A, biết B(7; -2) và C(1;4)
A.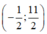 
B.(2;3)
C.(0;2)
D.(1;1)
Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho.
A. BM = a.
B. B M = a 2
C. B M = a 3
D. B M = a 5 2
Cho tam giác ABC có AB = c; BC = a; AC = b . Nếu giữa a; b; c có liên hệ b2 + c2 = 2a2 thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng:
A. a 3 2
B. a 3 3
C. a
D. 2a
Tam giác ABC có AB= AC= a ; A B C ^ = 120 ° . Tính độ dài vectơ tổng A B → + A C →
A. 
B. 
C. 
D. 
