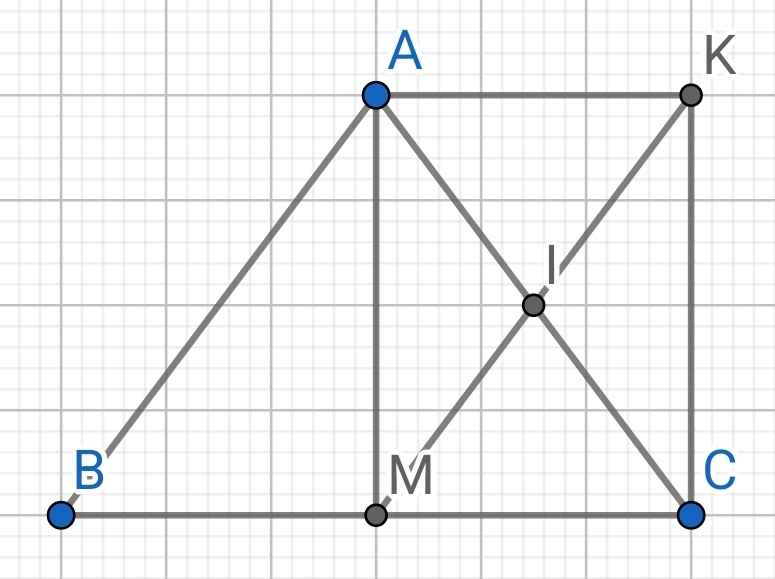
Cho tam giác ABC cân tại A. Điểm M và điểm I là thứ tự trung điểm của cạnh đáy BC và cạnh bên AC. Trên tia đối của tia IM lấy điểm K sao cho IM = IK.
a) Tứ giác AMCK là hình gì? Vì sao?
b) Chứng minh: AK // BC.
c) Chứng minh: Tứ giác ABMK là hình bình hành.
( Không sử dụng đường trung bình, các kiến thức trong sách cũ và chương IV!)
a) Do M là trung điểm BC (gt)
⇒ AM là đường trung tuyến của ∆ABC
Mà ∆ABC cân tại A (gt)
⇒ AM là đường cao của ∆ABC
⇒ AM ⊥ BC
⇒ AM ⊥ MC
⇒ ∠AMC = 90⁰
Do IM = IK (gt)
⇒ I là trung điểm của MK
Tứ giác AMCK có:
I là trung điểm của MK (cmt)
I là trung điểm của AC (gt)
⇒ AMCK là hình bình hành
Mà ∠AMC = 90⁰ (cmt)
⇒ AMCK là hình chữ nhật
b) Do AMCK là hình chữ nhật (cmt)
⇒ AK // MC
⇒ AK // BC
c) Do M là trung điểm của BC (gt)
⇒ BM = CM
Do AMCK là hình chữ nhật (cmt)
⇒ AK = CM
Mà BM = CM (cmt)
⇒ AK = BM
Do AK // BC (cmt)
⇒ AK // BM
Tứ giác ABMK có:
AK // BM (cmt)
AK = BM (cmt)
⇒ ABMK là hình bình hành














