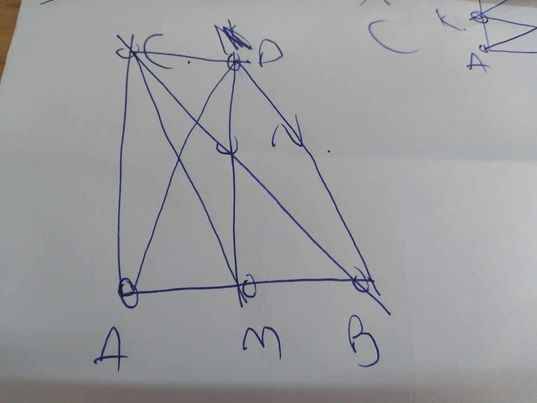
Cho tam giác ABC vuông tại A , có AB<AC . Gọi M và N thứ tự là trung điểm của AB và BC . Trên tia đối của tia NM lấy điểm D sao cho ND=NM.
a) Chứng minh: Tứ giác BMCD là hình bình hành .
b) Tứ giác AMDC là hình gì ? Vì sao?
c) Chúng minh : Tam giác BDA là tam giác cân
(vẽ hình và viết giả thuyết kết luận) giúp mình với m.n ơi mình đag cần gấp . Mình cảm ơn nhiều ạ!![]()
a: Xét tứ giác BMCD có
N là trung điểm chung của BC và MD
=>BMCD là hình bình hành
b: Ta có: BMCD là hình bình hành
=>BM//CD và BM=CD
Ta có: BM//CD
M\(\in\)AB
Do đó: AM//CD
ta có: BM=CD
AM=MB
Do đó: AM=CD
Xét tứ giác AMDC có
AM//DC
AM=DC
Do đó: AMDC là hình bình hành
Hình bình hành AMDC có \(\widehat{MAC}=90^0\)
nên AMDC là hình chữ nhật
c: Ta có: AMDC là hình chữ nhật
=>\(\widehat{DMA}=90^0\)
=>DM\(\perp\)AB tại M
Xét ΔDBA có
DM là đường cao
DM là đường trung tuyến
Do đó: ΔDBA cân tại D