Question

Cho tam giác ABC cân tại A; CP,BQ lần lượt là các đường phân giác của góc C và góc B (P thuộc AB,Q thuộc AC).Gọi O là giao điểm của CP và BQ.

A,CMR:tam giác OBC là tam giác cân.

B,CMR:đường thẳng AO đi qua trung điểm của BC,

C,CMR:CP=BQ và tam giác APQ là tam giác cân.

GIẢI GIÚP MÌNH BÀI NÀY VỚI Ạ.

Answer 1

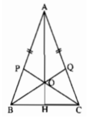
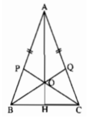
a: Ta có: \(\hat{ABQ}=\hat{CBQ}=\frac12\cdot\hat{ABC}\) (BQ là phân giác của góc ABC)

\(\hat{ACP}=\hat{BCP}=\frac12\cdot\hat{ACB}\) (CP là phân giác của góc ACB)

mà \(\hat{ABC}=\hat{ACB}\) (ΔABC cân tại A)

nên \(\hat{ABQ}=\hat{CBQ}=\hat{ACP}=\hat{BCP}\)

Xét ΔOBC có \(\hat{OBC}=\hat{OCB}\)

nên ΔOBC cân tại O

=>OB=OC

b: AB=AC
=>A nằm trên đường trung trực của BC(1)

OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra AO là đường trung trực của BC

=>AO đi qua trung điểm của BC

c: Xét ΔABQ và ΔACP có

\(\hat{ABQ}=\hat{ACP}\)

AB=AC
\(\hat{BAQ}\) chung

Do đó: ΔABQ=ΔACP

=>BQ=CP và AQ=AP

Xét ΔAPQ có AP=AQ
nên ΔAPQ cân tại A