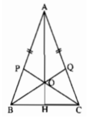
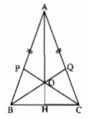
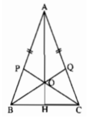
Gọi giao điểm AO với BC là H.
ΔAHB và ΔAHC có:
cạnh AH chung,
AB = AC
∠(BAH) = ∠(CAH) (theo b).
⇒ ΔAHB = ΔAHC (c.g.c)
⇒ HB = HC và ∠(AHB) = ∠(AHC)
Lại có: ∠(AHB) + ∠(AHC) = 180º ( hai góc kề bù)
Suy ra: ∠(AHB) = ∠(AHC) = 90º
tức là AO ⊥ BC và AO đi qua trung điểm của BC.