ΔOBC cân tại O ⇒ OB = OC.
ΔAOB và ΔAOC có: AO chung, AB = AC (giả thiết), OB = OC (cmt)
⇒ ΔAOB = ΔAOC (c.c.c).
⇒ ∠BAO = ∠CAO
⇒ AO là tia phân giác của góc BAC
⇒ O cách đều hai cạnh AB, AC
ΔOBC cân tại O ⇒ OB = OC.
ΔAOB và ΔAOC có: AO chung, AB = AC (giả thiết), OB = OC (cmt)
⇒ ΔAOB = ΔAOC (c.c.c).
⇒ ∠BAO = ∠CAO
⇒ AO là tia phân giác của góc BAC
⇒ O cách đều hai cạnh AB, AC
Cho tam giác cân ABC, AB = AC. Trên các cạnh AB, AC lần lượt lấy hai điểm P, Q sao cho AP = AQ. Hai đoạn thẳng CP, BQ cắt nhau tại O. Chứng minh rằng: Tam giác OBC là tam giác cân.
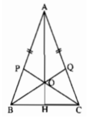
Cho tam giác cân ABC, AB = AC. Trên các cạnh AB, AC lần lượt lấy hai điểm P, Q sao cho AP = AQ. Hai đoạn thẳng CP, BQ cắt nhau tại O. Chứng minh rằng: AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.
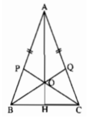
Cho tam giác cân ABC, AB=AC. Trên các cạnh AB, AC lần luợt lấy hai điểm P, Q sao cho Ap=AQ. Hai đoạn thẳng CP, BQ cắt nhau tại O. Chứng minh rằng:
a) Tam giác OBC là tam giác cân.
b) Điểm O cách đều hai cạnh AB, AC.
c) AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.
Cho tam giác cân ABC, AB=AC. Trên các cạnh AB, AC lần luợt lấy hai điểm P, Q sao cho Ap=AQ. Hai đoạn thẳng CP, BQ cắt nhau tại O. Chứng minh rằng:
a) Tam giác OBC là tam giác cân.
b) Điểm O cách đều hai cạnh AB, AC.
c) AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.
Cho tam giác ABC cân tại A. Trên các cạnh AB, AC lần lượt lấy hai điểm P, Q sao cho AP = AQ. Hai đoạn CP, BQ cắt nhau tại O.
Chứng minh rằng: O cách đều AB và AC. Giúp đỡ tui nhé các bạn
cho tam giác ABC cân tại A. Trên các cạnh AB,AC lần lượt lấy 2 điểm P,Q sao choAP=AQ. Hai đoạn thẳng CP,BQ cắt nhau tại điểm O. C/m tam giác AOB là tam giác cân.
Làm phiền các bạn wa
Cho tam giác ABC cân tại A. Trên cạnh AB và AC lần lượt lấy hai điểm P và Q sao cho AP = AQ. Gọi O là giao điểm của CP và BQ. Khi đó
A. OB = OC
B. O cách đều hai cạnh AB và AC
C. Tam giác OBC là tam giác cân
D. Cả A, B, C đều đúng
Cho tg ABC , AB = AC.Trên các cạnh AB , AC lần lượt lấy 2 điểm P , Q sao cho AP = AQ.Hai đoạn thẳng CP , BQ cắt nhau tại O .C/m rằng:
a) Tg OBC là tg cân.
b) Điểm O cách đều 2 cạnh AB , AC.
c) AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.
Cho tg ABC , AB = AC .Trên các cạnh AB , AC lần lượt lấy 2 điểm P , Q sao cho AP = AQ.Hai đoạn thẳng CP , BP cắt nhau tại O.C/m rằng:
a) Tg OBC cân
b) Điểm O cách đều 2 cạnh AB , AC.
c) AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.