Đáp án B
Phương pháp: Đặt t = 2 x
Cách giải: Đặt t = 2 x ta có:
![]()
Khi đó phương trình trở thành
![]()
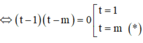
![]()
![]()
Để phương trình ban đầu có 3 nghiệm phân biệt ![]() có nghiệm
có nghiệm ![]()
Đáp án B
Phương pháp: Đặt t = 2 x
Cách giải: Đặt t = 2 x ta có:
![]()
Khi đó phương trình trở thành
![]()
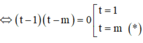
![]()
![]()
Để phương trình ban đầu có 3 nghiệm phân biệt ![]() có nghiệm
có nghiệm ![]()
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Tất cả các giá trị của m để phương trình f ( x ) - m + 1 = 0 có 4 nghiệm phân biệt là
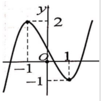
A. 0 < m < 1
B. 1 < m < 2
C. 2 < m < 3
D. m = 2
Cho hàm số y = f ( x ) = a x 4 + b x 2 + c ( a ≠ 0 ) có đồ thị như hình bên. Tất cả các giá trị của m để phương trình f x + m + 1 = 0 có 7 nghiệm phân biệt là:
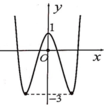
A. m = -2
B. m = -1
C. m = 2
D. m = 0
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Tất cả các giá trị của m để phương trình | f ( x ) | + m - 1 = 0 có 3 nghiệm phân biệt là
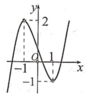
A. m=1
B. m=2
C. m = ± 1
D. m=0
Cho hàm số g ( x ) = x 2 + 1 và hàm số f ( x ) = x 3 - 3 x 2 + 1 . Tìm m để phương trình f ( g ( x ) ) - m = 0 có 4 nghiệm phân biệt.
A. - 3 < m < 1
B. - 3 < m ≤ 1
C. - 3 ≤ m ≤ - 1
D. m > - 1
Cho hàm số f ( x ) = ln x + x 2 + 1 Với mỗi số nguyên dương m đặt S m = f ( - m ) + f ( - m + 1 ) + . . + ( 0 ) + . . + f ( m - 1 ) Có bao nhiêu giá trị của m để phương trình 8 x - 3 . 4 x - S m = 0 có hai nghiệm thực phân biệt
A. 27
B. 2
C. 28
D. 1
Tìm m để phương trình cos2x + 2(m+1)sĩn -2m-1=0 có đúng 3 nghiệm x ∈ 0 ; π
![]()
![]()
![]()
![]()
Cho phương trình (ẩn x) x2 – 2(m – 1)x + m2 = 0.
a) Tính ∆'.
b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt ? Có nghiệm kép ? Vô nghiệm ?
Cho phương trình x 3 − 3 x 2 + 1 − m = 0 1 . Điều kiện của tham số m để phương trình (1) có ba nghiệm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 là
A. m = − 1
B. − 1 < m < 3
C. − 3 < m < − 1
D. − 3 ≤ m ≤ − 1