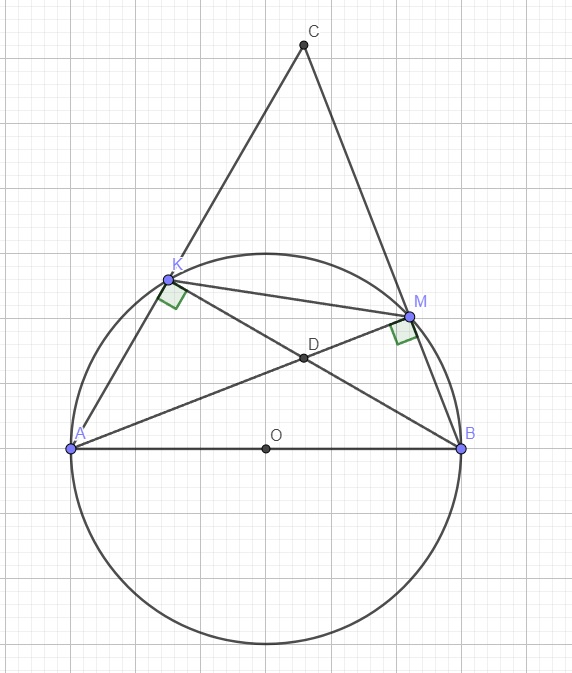
a.
Do AB là đường kính và K thuộc đường tròn \(\Rightarrow\widehat{AKB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{AKB}=90^0\Rightarrow\widehat{CKD}=180^0-\widehat{AKB}=90^0\) (1)
Tương tự ta có \(\widehat{AMB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{AMB}=90^0\Rightarrow\widehat{CMD}=180^0-\widehat{AMB}=90^0\) (2)
(1);(2)\(\Rightarrow K;M\) cùng nhìn CD dưới 1 góc vuông nên bốn điểm K, C, M, D cùng thuộc đường tròn đường kính CD
b.
Ta có: \(\left\{{}\begin{matrix}\widehat{AKB}=90^0\Rightarrow BK\perp AC\\\widehat{AMB}=90^0\Rightarrow AM\perp BC\end{matrix}\right.\)
Mà D là giao điểm BK và AM
\(\Rightarrow D\) là trực tâm tam giác ABC
\(\Rightarrow CD\) là đường cao thứ 3 của tam giác ABC
\(\Rightarrow CD\perp AB\)
c.
Xét hai tam giác DMB và DKA có:
\(\left\{{}\begin{matrix}\widehat{DMB}=\widehat{DKA}=90^0\\\widehat{BDM}=\widehat{ADK}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DMB\sim\Delta DKA\left(g.g\right)\)
\(\Rightarrow\dfrac{DM}{DK}=\dfrac{DB}{DA}\Rightarrow DK.DB=DM.DA\)
d.
Do ABMk nội tiếp (O) \(\Rightarrow\widehat{KAB}+\widehat{KMB}=180^0\)
Mà \(\widehat{CMK}+\widehat{KMB}=180^0\) (kề bù)
\(\Rightarrow\widehat{KAB}=\widehat{CMK}\) hay \(\widehat{CAB}=\widehat{CMK}\)
Xét hai tam giác CAB và CMK có:
\(\left\{{}\begin{matrix}\widehat{CAB}=\widehat{CMK}\left(cmt\right)\\\widehat{C}\text{ là góc chung}\end{matrix}\right.\)
\(\Rightarrow\Delta CAB\sim\Delta CMK\left(g.g\right)\)
\(\Rightarrow\dfrac{CA}{CM}=\dfrac{CB}{CK}\Rightarrow CK.CA=CM.CB\)