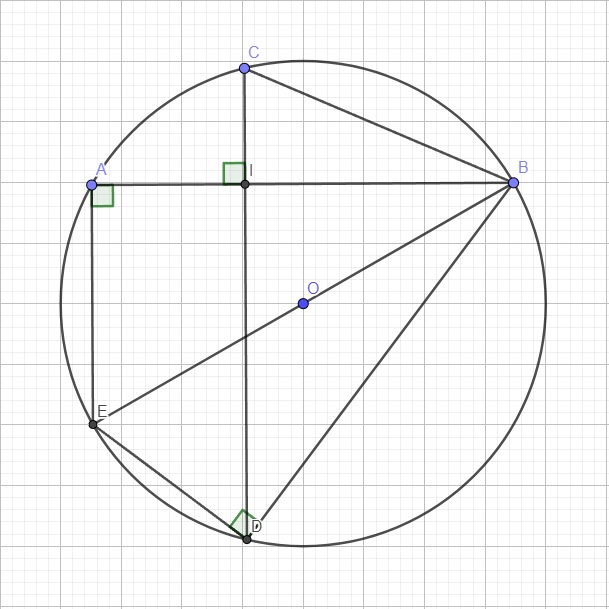
a.
Do BE là đường kinh \(\Rightarrow\widehat{BAE}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{BAE}=90^0\) hay \(AB\perp AE\)
\(\Rightarrow CD||AE\) (cùng vuông góc AB)
\(\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{DE}\Rightarrow AC=DE\)
b.
BE là đường kính nên \(\widehat{BDE}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{BDE}=90^0\Rightarrow\Delta BDE\) vuông tại D \(\Rightarrow BD^2+DE^2=BE^2\)
Áp dụng định lý Pitago cho 2 tam giác vuông IAC và IBD:
\(\left(IA^2+IC^2\right)+\left(IB^2+ID^2\right)=AC^2+BD^2=DE^2+BD^2=BE^2=\left(2R\right)^2=4R^2\)