được nhma phải chứng minh và bài chứng minh có thể bị đánh sai vì một số trường hợp khác
Đúng 0
Bình luận (1)
Các câu hỏi tương tự
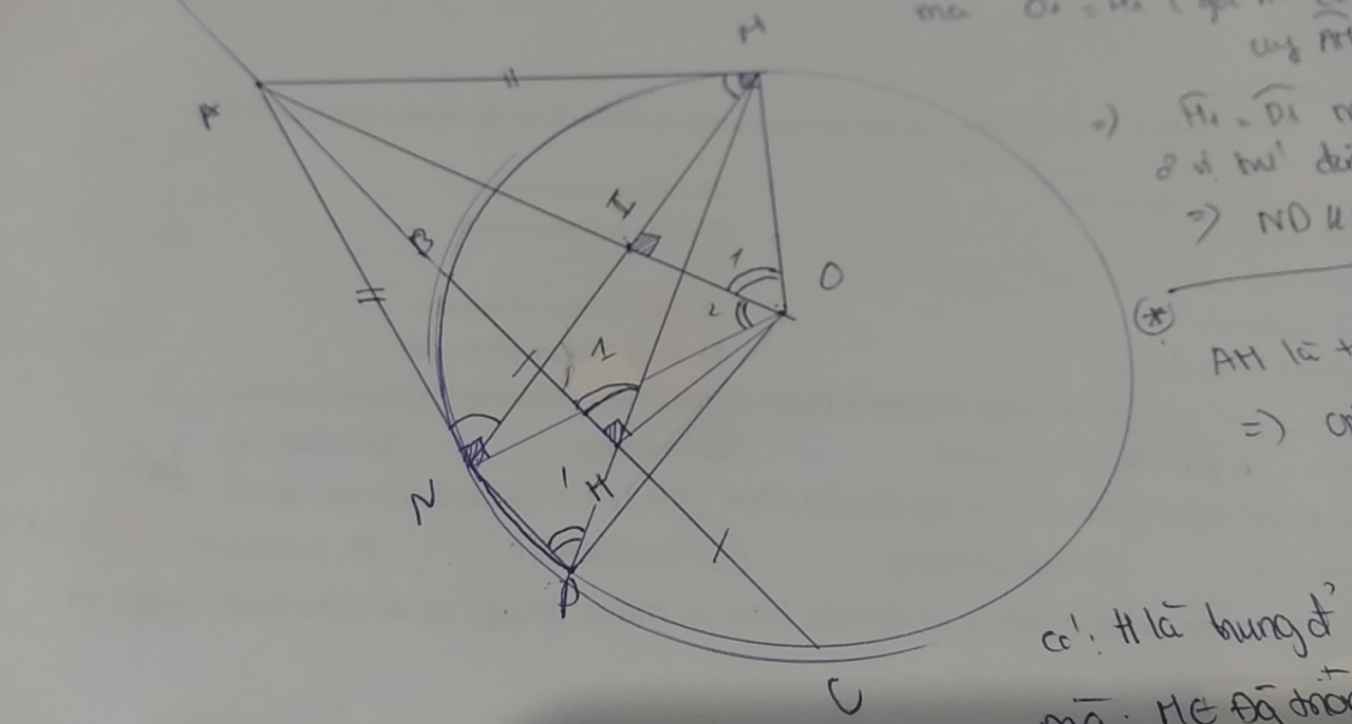
giúp em với nhacho tam giác ABC nội tiếp đường tròn (O) (ABAC) . Phân giác trong của góc A cắt (O) ở M , phân giác ngoài của góc A cắt (O) tại N . a . CM : MN vuông góc BCb. gọi O1 , O2 lần lượt là tâm đường tròn ngoại tiếp tam giác ABD ; ACD . CM : MB là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD và B; O1 ; N thẳng hàngc . chứng minh : tam giác AO1O2 đồng dạng ABCd . CM : OO1 OO2
Đọc tiếp
giúp em với nha
cho tam giác ABC nội tiếp đường tròn (O) (AB<AC) . Phân giác trong của góc A cắt (O) ở M , phân giác ngoài của góc A cắt (O) tại N .
a . CM : MN vuông góc BC
b. gọi O1 , O2 lần lượt là tâm đường tròn ngoại tiếp tam giác ABD ; ACD . CM : MB là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD và B; O1 ; N thẳng hàng
c . chứng minh : tam giác AO1O2 đồng dạng ABC
d . CM : OO1 = OO2
Cho tam giác ABC có 3 góc nhọn ( AB<AC) nội tiếp đường tròn tâm O. Kẻ đường cao AD và đường kính AA'. Gọi E,F theo thứ tự là chân đường vuông góc hạ từ B và C xuống đường kính AA',gọi M là trung điểm BC.CM MD=ME=MF ( AEDB nt;DB.AC=AD.A'C; DE//A'C )
Cho tam giác ABC cân tại A, có O là trung điểm BC và BC2a. Đường tròn tâm O tiếp xúc với AB, AC lần lượt tại H và T. Qua D trên cung nhỏ HT, kẻ tiếp tuyến với (O) cắt AB và AC ở M và Na) Xác định tâm I của đường tròn ngoại tiếp tam giác AHTb) Chứng minh góc MON góc ABCc) Tính tích BM.CN theo ad) Định vị trí của MN sao cho BM+CN đạt giá trị nhỏ nhấtGiup với mình tick cho
Đọc tiếp
Cho tam giác ABC cân tại A, có O là trung điểm BC và BC=2a. Đường tròn tâm O tiếp xúc với AB, AC lần lượt tại H và T. Qua D trên cung nhỏ HT, kẻ tiếp tuyến với (O) cắt AB và AC ở M và N
a) Xác định tâm I của đường tròn ngoại tiếp tam giác AHT
b) Chứng minh góc MON= góc ABC
c) Tính tích BM.CN theo a
d) Định vị trí của MN sao cho BM+CN đạt giá trị nhỏ nhất
Giup với mình tick cho
Cho tam giác ABC nội tiếp đường tròn tâm O, có góc C=450. Đường tròn đường kính AB cắt các cạnh AC và BC lần lượt ở M và N.
a. Chứng minh rằng MN vuông góc với OC
b. Cho AB=2a. Tính MN
Cho tam giác ABC, góc A= α; phân giác trong của góc B và góc C gặp nhau ở M. phân giác ngoài của góc B và góc C gặp nhau ở N
a) Tính góc BMC và góc BNC theo α
b) c/m B,M,C,N thuộc đường tròn tâm O. Tìm vị trí của O
c) Tính số đo cung BMC và số đo cung BNC của (O)
Cho tam giác ABC, góc A= α; phân giác trong của góc B và góc C gặp nhau ở M. phân giác ngoài của góc B và góc C gặp nhau ở N
a) Tính góc BMC và góc BNC theo α
b) c/m B,M,C,N thuộc đường tròn tâm O. Tìm vị trí của O
c) Tính số đo cung BMC và số đo cung BNC của (O)
Cho tam giác ABC vuông ở A có AH là đường cao và BE là đường phân giác (H thuộc BC, E thuộc AC). Kẻ AD vuông góc với BE tại H.
a) CM AHBD nt đường tròn (o) và xác định tâm O
b) CM OD vuông góc với AH
c) CM HDC=CEH
Cho đường tròn tâm O bán kính R. Vẽ góc ở tâm AOB = 80 ° , vẽ góc ở tâm BOC = 120 ° kề với góc AOB. So sánh và sắp xếp độ dài AB, BC, CA theo thứ tự tăng dần.
cho hình chữ nhật ABCD nội tiếp đường tròn tâm O . Tia phân giác góc ACD cắt cung nhỏ AD của đường tròn tâm O tại điểm H .
a. chứng minh 3 điểm A , O , C thẳng hàng và HA = HD
b. Dây HC cắt BD tại M , dây HB cắt AC tại N . Chứng minh tứ giác MNBC nt và MN vuông góc OH
c. Dây HB cắt AD tại I . chứng minh IA < ID và AB . AC = BH . BI