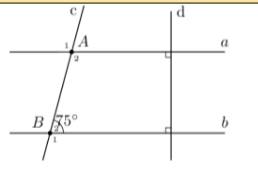
Do \(a\perp d\) và \(b\perp d\)
\(\Rightarrow a\) // \(b\)
Ta có:
\(\widehat{B_1}+\widehat{B_2}=180^0\) (kề bù)
\(\Rightarrow\widehat{B_1}=180^0-\widehat{B_2}=180^0-75^0=105^0\)
Do \(a\) // \(b\)
\(\Rightarrow\widehat{A_2}=\widehat{B_1}=105^0\) (đồng vị)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}=105^0\) (đối đỉnh)
a vuông góc d
b vuông góc d
=>a//b
=>góc B2+góc A2=180 độ(hai góc trong cùng phía)
=>góc A2=105 độ
góc B2+góc B1=180 độ(hai góc kề bù)
=>góc B1=180 độ-góc B2=105 độ
góc A2=góc A1(hai góc đối đỉnh)
mà góc A2=105 độ
nên góc A1=105 độ
Ta có:
\(\left\{{}\begin{matrix}a\perp d\\b\perp d\end{matrix}\right.\)
\(\Rightarrow a//b\)
\(\Rightarrow\widehat{B_2}+\widehat{A_2}=180^o\) (trong cùng phía)
\(\Rightarrow\widehat{A_2}=180^o-\widehat{B_2}=180^o-75^o=105^o\)
Mà: \(\widehat{A_1}\) đối đỉnh \(\widehat{A_2}\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}=105^o\)
Và: \(\widehat{B_1}+\widehat{B_2}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{B_1}=180^o-\widehat{B_2}=180^o-75^o=105^o\)