Chọn C
Vì thiết diện cắt bởi mặt phẳng qua trục là hình vuông nên khối trụ có chiều cao bằng 2r. Ta có
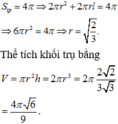
Chọn C
Vì thiết diện cắt bởi mặt phẳng qua trục là hình vuông nên khối trụ có chiều cao bằng 2r. Ta có
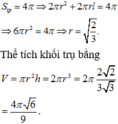
Cho hình trụ có diện tích toàn phần là 4 π và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Thể tích khối trụ đã cho bằng
A. 4 π 6 9
B. π 6 12
C. π 6 9
D. 4 π 9
Cho hình trụ có diện tích xung quanh bằng 4 π , thiết diện qua trục là hình vuông. Tính thể tích V của khối trụ giới hạn bởi hình trụ
A. V = 2 π
B. V = 6 π
C. V = 3 π
D. V = 5 π
Cho hình trụ có diện tích toàn phần là 4π và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ.
A. 4 π 9
B. π 6 9
C. 4 π 6 9
D. π 6 12
Cho hình trụ có diện tích toàn phần là 8ᴨ và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ?
A. 4 π 9
B. π 6 9
C. 16 π 3 9
D. π 6 12
Cho hình trụ có diện tích toàn phần là 4 π và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ.
A. π 6 9
B. 4 π 6 9
C. π 6 12
D. 4 π 9
Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần S t p của khối trụ.
A. S t p = 27 π a 2 2 .
B. S t p = 13 a 2 π 6 .
C. S t p = a 2 π 3 .
D. S = a 2 π 3 2 .
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3.a Tính diện tích toàn phần của hình trụ đã cho
A. 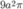
B. 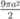
C. 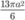
D. 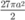
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác đều cạnh là 2 sin x
A. V = 3
B. V = 3 π
C. V = - 2 π 3
D. V = 2 3
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác đều cạnh là 2 s i n x
A. V = 3
B. V = 3 π
C. V = 2 π 3
D. V = 2 3