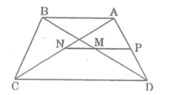
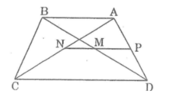
a: Gọi K,E lần lượt là trung điểm của AD,BC
Xét ΔDAB có
K,M lần lượt là trung điểm của DA,DB
=>KM là đường trung bình của ΔDAB
=>KM//AB và \(KM=\frac{AB}{2}\)
Xét ΔCAB có
N,E lần lượt là trung điểm của CA,CB
=>NE là đường trung bình của ΔCAB
=>NE//AB và \(NE=\frac{AB}{2}\)
Xét hình thang ABCD có
K,E lần lượt là trung điểm của AD,BC
=>KE là đường trung bình của hình thang ABCD
=>KE//AB//CD và \(KE=\frac{AB+CD}{2}\)
Ta có: KE//AB
NE//AB
KE,NE có điểm chung là E
Do đó: K,N,E thẳng hàng
Ta có: KM//AB
KE//AB
KM,KE có điểm chung là K
Do đó: K,M,E thẳng hàng
mà K,N,E thẳng hàng
nên K,M,N,E thẳng hàng
=>MN//AB
b: Xét ΔOAB và ΔOCD có
\(\hat{OAB}=\hat{OCD}\) (hai góc so le trong, AB//CD)
\(\hat{AOB}=\hat{COD}\) (hai góc đối đỉnh)
Do đó: ΔOAB~ΔOCD
=>\(\frac{OA}{OC}=\frac{OB}{OD}\)
=>\(\frac{OA}{OB}=\frac{OC}{OD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{OA}{OB}=\frac{OC}{OD}=\frac{OA+OC}{OB+OD}=\frac{AC}{BD}\)
=>\(\frac{OA}{OB}=\frac{AC}{BD}=\frac{2\cdot NC}{2\cdot MD}=\frac{NC}{MD}\)
c: Ta có: KM+MN+NE=KE
=>\(MN+\frac{AB}{2}+\frac{AB}{2}=\frac12\left(AB+CD\right)\)
=>\(MN=\frac12\left(AB+CD-AB-AB\right)=\frac12\left(CD-AB\right)\)