Do \(AC||A'C'\Rightarrow\widehat{\left(AD;A'C'\right)}=\widehat{\left(AD;AC\right)}=\widehat{CAD}=45^0\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
cho hình lập phương ABCD.A'B'C'D' và M,N,E,F lần lượt là trung điểm các cạnh BC, BA, AA' , A'D'. Tính góc giữa các cặp đường thẳng sau
a) A'C' và BC
b) MN và EF
c) MN và BC
d) EF và CC'
Cho hình lập phương ABCD.ABCD có khoảng cách giữa AC và CD là 1 cm. Thể tích khối lập phương ABCD.ABCD là: A. 8
c
m
3
. B.
2
2
c
m
3
. C.
3...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có khoảng cách giữa A'C và C'D' là 1 cm. Thể tích khối lập phương ABCD.A'B'C'D' là:
A. 8 c m 3 .
B. 2 2 c m 3 .
C. 3 3 c m 3 .
D. 27 c m 3
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính góc giữa hai đường thẳng BD và AC
A . 60 0
B . 30 0
C . 45 0
D . 90 0
Cho hình hộp ABCD.ABCD có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng
60
0
. Tính khoảng cách giữa hai đường thẳng AB và AC
A
.
22
11
B
.
2
11
C
.
2
11
D
.
...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 0 . Tính khoảng cách giữa hai đường thẳng AB' và A'C'
A . 22 11
B . 2 11
C . 2 11
D . 3 11
cho hình lập phương abcd.a'b'c'd' gọi I là trung điểm cạnh AB. Tính cosin của góc giữa hai đường thẳng A'D và B'I được kết quả là
Cho hình lập phương ABCD.ABCD. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CD. Xác định góc giữa hai đường thẳng MN và AP A.
60
0
B.
90
0
C.
30
0
D.
45
0
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Xác định góc giữa hai đường thẳng MN và AP
A. 60 0
B. 90 0
C. 30 0
D. 45 0
Cho hình lập phương ABCD.A'B'C'D'
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
Cho hình lập phương ABCD.ABCD (tham khảo hình vẽ bên). Tang góc giữa đường thẳng BD′BD′ và mặt phẳng (ADDA) bằng A.
3
3
B.
6
3
C.
2
2
D.
2...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' (tham khảo hình vẽ bên). Tang góc giữa đường thẳng BD′BD′ và mặt phẳng (ADD'A') bằng
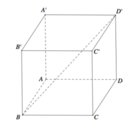
A. 3 3
B. 6 3
C. 2 2
D. 2 6
Cho hình lập phương ABCD.ABCD cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và AD bằng A.
a
2
2
B. a. C.
a
2
D.
a
3
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và A'D' bằng
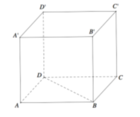
A. a 2 2
B. a.
C. a 2
D. a 3






