Đáp án B
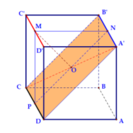
Gọi M là trung điểm C’D’. Đặt x là cạnh của hình lập phương
Ta có
![]()
![]()
![]()
Gọi O là trung điểm A’C. Dễ dàng chứng minh OM ⊥ (A'B'CD) (xin dành cho bạn đọc).
Suy ra
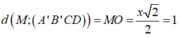
![]()
Đáp án B
Gọi M là trung điểm C’D’. Đặt x là cạnh của hình lập phương
Ta có
![]()
![]()
![]()
Gọi O là trung điểm A’C. Dễ dàng chứng minh OM ⊥ (A'B'CD) (xin dành cho bạn đọc).
Suy ra
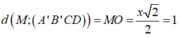
![]()

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN
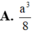
![]()
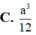
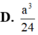
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB, C'D' bằng
A. a
B. a 2
C. a 3
D. a 3 2
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Xác định góc giữa hai đường thẳng MN và AP
A. 60 0
B. 90 0
C. 30 0
D. 45 0
Cho hình lập phương ABCD.A' B' C' D' có A'C = 3 a 3 . Thể tích của khối lập phương ABCD.A' B' C' D' là
A. 9 a 3 3
B. 27 a 3
C. 3 a 3
D. a 3
Cho hình lập phương ABCD.A'B'C'D'. GÓC GIỮA HAI ĐƯỜNG THẲNG AD và A'C' là
Cho hình lập phương ABCD.A'B'C'D'
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, C, D, A', B' và D' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó.
cho hình lập phương ABCD.A'B'C'D' và M,N,E,F lần lượt là trung điểm các cạnh BC, BA, AA' , A'D'. Tính góc giữa các cặp đường thẳng sau
a) A'C' và BC
b) MN và EF
c) MN và BC
d) EF và CC'
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuôngA'B'C'D'. Kết quả tính diện tích toàn phần S t p của khối nón đó có dạng πa 2 4 ( b + c ) với b và c là hai số nguyên dương và b>1. Tính bc
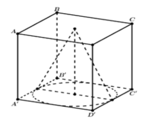
A. bc=5
B. bc=7
C.bc=8
D.bc=15