Các câu hỏi tương tự
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có
A
0
;
0
;
0
,
B
1
;
0
;
0...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có A 0 ; 0 ; 0 , B 1 ; 0 ; 0 , D 0 ; 1 ; 0 v à A ' 0 ; 0 ; 1 . Gọi P : a x + b y + c z + d = 0 là mặt phẳng chứa đường thẳng CD' và tạo với mặt phẳng (BB'D'D) góc nhỏ nhất. Cho T = a + 2 b + 3 c + 4 d . Tìm giá trị nguyên âm lớn nhất của T biết a là số nguyên.
A. -1
B. -2
C. -6
D. -4
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADDA. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng A.
3
5
4
14
B.
14...
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A'. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
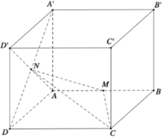
A. 3 5 4 14
B. 14 4
C. 3 14 4 5
D. 9 4 14
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x+2y-2z-100 với hai điểm A(1;2;0), B(-1;3;1). Gọi (Q) là một mặt phẳng đi qua A, B đồng thời tạo với (P) một góc nhỏ nhất. Biết rằng phương trình tổng quát của mặt phẳng (Q) là: ax+by+cz+d0 với a, b, c, d là những số thực, Khi đó giá trị của tổng S b + c + d bằng A. 10 B. 12 C. 18 D. -8
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x+2y-2z-10=0 với hai điểm A(1;2;0), B(-1;3;1). Gọi (Q) là một mặt phẳng đi qua A, B đồng thời tạo với (P) một góc nhỏ nhất. Biết rằng phương trình tổng quát của mặt phẳng (Q) là: ax+by+cz+d=0 với a, b, c, d là những số thực, Khi đó giá trị của tổng S = b + c + d bằng
A. 10
B. 12
C. 18
D. -8
Trong không gian với hệ tọa độ Oxyz, biết mặt phẳng (P):6 +by +cz -1 0 với c 0 đi qua hai điểm A(0;1;0), B(1;0;0) và tạo với mặt phẳng (yOz) một góc 60 độ Khi đó giá trị a + b +c thuộc khoảng nào dưới đây? A. (0;3). B. (3;5). C. (5;8). D. (8;11).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, biết mặt phẳng (P):6 +by +cz -1 =0 với c < 0 đi qua hai điểm A(0;1;0), B(1;0;0) và tạo với mặt phẳng (yOz) một góc 60 độ Khi đó giá trị a + b +c thuộc khoảng nào dưới đây?
A. (0;3).
B. (3;5).
C. (5;8).
D. (8;11).
Cho hình lập phương
A
B
C
D
.
A
B
C
D
. Xét (P) là mặt phẳng thay đổi luôn chứa đường thẳng
C
D
. Giá trị nhỏ nhất của số đo góc giữa mặt phẳng (P) và mặt phẳng (
B
D
D
B
) bằng A.
60
0
B.
30...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' . Xét (P) là mặt phẳng thay đổi luôn chứa đường thẳng C D ' . Giá trị nhỏ nhất của số đo góc giữa mặt phẳng (P) và mặt phẳng ( B D D ' B ' ) bằng
A. 60 0
B. 30 0
C. 45 0
D. 0 0
Trong không gian với hệ tọa độ Oxyz cho hình lập phương ABCD.A’B’C’D’ có A(0;0;0), B(1;0;0), D(0;1;0) và A(0;0;1). Khoảng cách giữa AC và B’D là A.
1
3
.
B.
1
6
.
C. 1 D.
2
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hình lập phương ABCD.A’B’C’D’ có A(0;0;0), B(1;0;0), D(0;1;0) và A'(0;0;1). Khoảng cách giữa AC và B’D là
A. 1 3 .
B. 1 6 .
C. 1
D. 2 .
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A B (3; 2;6), (0;1;0) - và mặt cầu (S): . Mặt phẳng (P): ax + by + cz – 2 0 đi qua A, B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T a + b + c A. T 5 B. T 3 C. T 2 D. T 4
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A B (3; 2;6), (0;1;0) - và mặt cầu (S): 
. Mặt phẳng (P): ax + by + cz – 2 = 0 đi qua A, B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T = a + b + c
A. T = 5
B. T = 3
C. T = 2
D. T = 4
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;1;2), M(3;0;0) và mặt phẳng (P):x+y+z-30. Đường thẳng
∆
đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ điểm A đến đường thẳng
∆
là nhỏ nhất. Gọi
u
→
a
,
b
,
c
là vectơ chỉ phương của
∆
với a, b, c là các số nguyên có ước...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;1;2), M(3;0;0) và mặt phẳng (P):x+y+z-3=0. Đường thẳng ∆ đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ điểm A đến đường thẳng ∆ là nhỏ nhất. Gọi u → = a , b , c là vectơ chỉ phương của ∆ với a, b, c là các số nguyên có ước chung lớn nhất bằng 1. Tính giá trị T=a+b+c.
A. T = -1
B. T = 1.
C. T = 0.
D. T = 2.
Trong không gian Oxyz, cho hai điểm A (1;2;4), B (0;0;1) và mặt cầu
S
:
x
+
1
2
+
y
-
1
2
+
z
2
4
. Mặt phẳng
P
:
a
x...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A (1;2;4), B (0;0;1) và mặt cầu S : x + 1 2 + y - 1 2 + z 2 = 4 . Mặt phẳng P : a x + b y + c z + 3 = 0 đi qua A, B và cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính T = a + b + c
A. T = - 3 4
B. T = 33 5
C. T = 27 4
D. T = 31 5