Các câu hỏi tương tự
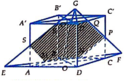
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng AA’,BB’,CC’ thỏa mãn diện tích của tam giác MNP bằng
a
2
. Góc giữa hai mặt phẳng (MNP) và (ABCD) là A.
60
o
B.
30
o
C.
45
o
D.
120
o
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng AA’,BB’,CC’ thỏa mãn diện tích của tam giác MNP bằng a 2 . Góc giữa hai mặt phẳng (MNP) và (ABCD) là
A. 60 o
B. 30 o
C. 45 o
D. 120 o
Cho hình lập phương ABCD.A′B′C′D′ có độ dài cạnh bằng 3. Một mặt phẳng (α) đồng thời cắt các cạnh AA′,BB′,CC′,DD′ lần lượt tại các điểm M,N,P,Q. Diện tích tứ giác MNPQ bằng 18. Góc giữa (α) và mặt phẳng đáy bằng A.
45
°
B.
30
°
C.
60
°
D.
0
°
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có độ dài cạnh bằng 3. Một mặt phẳng (α) đồng thời cắt các cạnh AA′,BB′,CC′,DD′ lần lượt tại các điểm M,N,P,Q. Diện tích tứ giác MNPQ bằng 18. Góc giữa (α) và mặt phẳng đáy bằng
A. 45 °
B. 30 °
C. 60 °
D. 0 °
Cho hình lăng trụ đều ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Mặt phẳng (α) lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng (α) và mặt phẳng (ABCD) là 600. Diện tích tứ giác MNPQ là : A.
2
3
a
2
B.
1
2...
Đọc tiếp
Cho hình lăng trụ đều ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Mặt phẳng (α) lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng (α) và mặt phẳng (ABCD) là 600. Diện tích tứ giác MNPQ là :
A. 2 3 a 2
B. 1 2 a 2
C. 2 a 2
D. 3 2 a 2
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng A.
7
a
2
3
48
B.
7
a
2
3
24
C. ...
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
A. 7 a 2 3 48
B. 7 a 2 3 24
C. a 2 3 16
D. a 2 3 48
Trong không gian Oxyz, cho tam giác nhọn ABC có H(2;2;1),
K
−
8
3
;
4
3
;
8
3
, O lần lượt là hình chiếu vuông góc của A, B, C trên các cạnh BC, AC, AB. Đường thẳng d qua A và vuông góc với mặt phẳng (ABC) có phư...
Đọc tiếp
Trong không gian Oxyz, cho tam giác nhọn ABC có H(2;2;1), K − 8 3 ; 4 3 ; 8 3 , O lần lượt là hình chiếu vuông góc của A, B, C trên các cạnh BC, AC, AB. Đường thẳng d qua A và vuông góc với mặt phẳng (ABC) có phương trình là
A. d : x 1 = y − 6 − 2 = z − 6 2
B. d : x − 8 3 1 = y − 2 3 − 2 = z + 2 3 2
C. d : x + 4 9 1 = y − 17 9 − 2 = z − 19 9 2
D. d : x + 4 1 = y + 1 − 2 = z − 1 2
Cho hình chóp tứ giác S.ABCD đáy là hình bình hành có thể tích bằng V. Lấy điểm B, D lần lượt là trung điểm của các cạnh SB và SD. Mặt phẳng (ABD) cắt cạnh SC tại C. Khi đó thể tích khối chóp S.ABCD bằng A.
V
3
B.
2
V
3
C.
V
3
3
D.
V
6
Đọc tiếp
Cho hình chóp tứ giác S.ABCD đáy là hình bình hành có thể tích bằng V. Lấy điểm B', D' lần lượt là trung điểm của các cạnh SB và SD. Mặt phẳng (AB'D') cắt cạnh SC tại C'. Khi đó thể tích khối chóp S.AB'C'D' bằng
A. V 3
B. 2 V 3
C. V 3 3
D. V 6
Cho tam giác ABC(góc A=90o) có M là trung điểm của BC. Điểm D và E là các điểm đối xứng với M qua AB và AC; MD cắt AB ở F;ME cắt AC ở N.
a) Tứ giác AFMN là hình gì? Vì sao?
b) Chứng minh tứ giác ADBM là hình thoi
c) Chứng minh A là trung điểm của DE
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là: A.
a
2
11
2
B.
a
2
2
4
C. ...
Đọc tiếp
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:
A. a 2 11 2
B. a 2 2 4
C. a 2 11 4
D. a 2 3 4
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADDA. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng A.
3
5
4
14
B.
14...
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A'. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
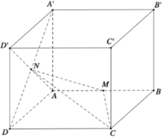
A. 3 5 4 14
B. 14 4
C. 3 14 4 5
D. 9 4 14