Đáp án C
Phương pháp : Sử dụng công thức ![]()
Cách giải :
![]()
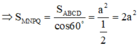
Đáp án C
Phương pháp : Sử dụng công thức ![]()
Cách giải :
![]()
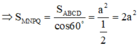
Cho hình lập phương ABCD.A′B′C′D′ có độ dài cạnh bằng 3. Một mặt phẳng (α) đồng thời cắt các cạnh AA′,BB′,CC′,DD′ lần lượt tại các điểm M,N,P,Q. Diện tích tứ giác MNPQ bằng 18. Góc giữa (α) và mặt phẳng đáy bằng
A. 45 °
B. 30 °
C. 60 °
D. 0 °
Cho hình lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc α là góc giữa hai đường thẳng AA’ và BM
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, tam giác SAB đều. Gọi M là điểm trên cạnh AD sao cho A M = x ; x ∈ 0 ; a . Mặt phẳng α đi qua M và song song với (SAB) lần lượt cắt các cạnh CB, CS, SD tại N, P, Q. Tìm x để diện tích tứ giác MNPQ bằng 2 a 2 3 9
A. 2 a 3
B. a 4
C. a 2
D. a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy. Mặt phẳng ( α ) qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP là
A. V = 32 π 3
B. 64 2 π 3
C. 108 π 3
D. 125 π 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt đáy. Mặt phẳng α qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
A. V = 108 π 3
B. V = 64 2 π 3
C. V = 125 π 6
D. V = 32 π 3
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm H của A’B’. Gọi M, N lần lượt là trung điểm của AA’, B’C’. Biết rằng AH = 2a và α là số đo của góc giữa đường thẳng MN và mặt phẳng (AC’H). Khi đó cosα bằng
A. 77 11
B. 22 11
C. 2 5 5
D. 5 5
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng AA’,BB’,CC’ thỏa mãn diện tích của tam giác MNP bằng a 2 . Góc giữa hai mặt phẳng (MNP) và (ABCD) là
A. 60 o
B. 30 o
C. 45 o
D. 120 o
Cho hình lăng trụ ABC.A’B’C’ có A’.ABC là tứ diện đều cạnh a. Gọi M,N lần lượt là trung điểm của AA’ và BB’. Tính tan của góc giữa hai mặt phẳng (ABC) và (CMN).
A. 2 5
B. 3 2 4
C. 2 2 5
D. 4 2 5